
【题目】在ABCD中,点B关于AD的对称点为B′,连接AB′,CB′,CB′交AD于F点.
(1)如图1,∠ABC=90°,求证:F为CB′的中点;
(2)小宇通过观察、实验、提出猜想:如图2,在点B绕点A旋转的过程中,点F始终为CB′的中点.小宇把这个猜想与同学们进行交流,通过讨论,形成了证明该猜想的几种想法:
想法1:过点B′作B′G∥CD交AD于G点,只需证三角形全等;
想法2:连接BB′交AD于H点,只需证H为BB′的中点;
想法3:连接BB′,BF,只需证∠B′BC=90°.
…
请你参考上面的想法,证明F为CB′的中点.(一种方法即可)
(3)如图3,当∠ABC=135°时,AB′,CD的延长线相交于点E,求 ![]() 的值.
的值.
【答案】
(1)
解:证明:
∵四边形ABCD为平行四边形,∠ABC=90°,
∴□ABCD为矩形,AB=CD,
∴∠D=∠BAD=90°,
∵B,B′关于AD对称,
∴∠B′AD=∠BAD=90°,AB=AB′,
∴∠B′AD=∠D,
∵∠AFB′=∠CFD,
在△AFB′与△CFD中, 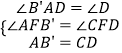 ,
,
∴△AFB′≌△CFD(AAS),
∴FB′=FC,
∴F是CB′的中点
(2)
解:证明:
方法1:如图2,

过点B′作B′G∥CD交AD于点G,
∵B,B′关于AD对称,
∴∠1=∠2,AB=AB′,
∵B′G∥CD,AB∥CD,
∴B′G∥AB.
∴∠2=∠3,
∴∠1=∠3,
∴B′A=B′G,
∵AB=CD,AB=AB′,
∴B′G=CD,
∵B′G∥CD,
∴∠4=∠D,
∵∠B′FG=∠CFD,
在△B′FG与△CFD中 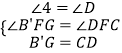 ,
,
∴△B′FG≌△CFD(AAS),
∴FB′=FC,
∴F是CB′的中点;
方法2:连接BB′交直线AD于H点,

∵B,B′关于AD对称,
∴AD是线段B′B的垂直平分线,
∴B′H=HB,
∵AD∥BC,
∴ ![]() =
= ![]() =1,
=1,
∴FB′=FC.
∴F是CB′的中点;
方法3:连接BB′,BF,

∵B,B′关于AD对称,
∴AD是线段B′B的垂直平分线,
∴B′F=FB,
∴∠1=∠2,
∵AD∥BC,
∴B′B⊥BC,
∴∠B′BC=90°,
∴∠1+∠3=90°,∠2+∠4=90°,
∴∠3=∠4,
∴FB=FC,
∴B′F=FB=FC,
∴F是CB′的中点;
(3)
解:取B′E的中点G,连结GF,

∵由(2)得,F为CB′的中点,
∴FG∥CE,FG= ![]() CE,
CE,
∵∠ABC=135°,□ABCD中,AD∥BC,
∴∠BAD=180°﹣∠ABC=45°,
∴由对称性,∠EAD=∠BAD=45°,
∵FG∥CE,AB∥CD,
∴FG∥AB,
∴∠GFA=∠FAB=45°,
∴∠FGA=90°,GA=GF,
∴FG=sin∠EADAF= ![]() AF,
AF,
∴由①,②可得 ![]() =
= ![]() .
.
【解析】(1)证明:根据已知条件得到□ABCD为矩形,AB=CD,根据矩形的性质得到∠D=∠BAD=90°,根据全等三角形的性质即可得到结论;(2)方法1:如图2,过点B′作B′G∥CD交AD于点G,由轴对称的性质得到∠1=∠2,AB=AB′,根据平行线的性质得到∠2=∠3,∠1=∠3,根据平行线的性质得到∠4=∠D,根据全等三角形的性质即可得到结论;方法2:连接BB′交直线AD于H点,根据线段垂直平分线的性质得到B′H=HB,由平行线分线段成比例定理得到结论;方法3:连接BB′,BF,根据轴对称的性质得到AD是线段B′B的垂直平分线,根据线段垂直平分线的性质得到B′F=FB,得到∠1=∠2,由平行线的性质得到∠B′BC=90°,根据余角的性质得到∠3=∠4,于是得到结论;(3)取B′E的中点G,连结GF,由(2)得,F为CB′的中点,根据平行线的性质得到∠BAD=180°﹣∠ABC=45°,由对称性的性质得到∠EAD=∠BAD=45°,根据平行线的性质得到∠GFA=∠FAB=45°,根据三角函数的定义即可得到结论.
【考点精析】本题主要考查了全等三角形的性质和相似三角形的性质的相关知识点,需要掌握全等三角形的对应边相等; 全等三角形的对应角相等;对应角相等,对应边成比例的两个三角形叫做相似三角形才能正确解答此题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图1,在矩形MNPQ中,动点R从点N出发,沿着N→P→Q→M方向运动至点M处停下,设点R运动的路程为x,△MNR的面积为y,如果y关于x的函数图象如图2所示,则下列说法不正确的是( )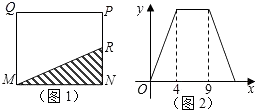
A.当x=2时,y=5
B.矩形MNPQ的面积是20
C.当x=6时,y=10
D.当y= ![]() 时,x=3
时,x=3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直线AB上任取一点O,过点O作射线OC、OD,使∠COD=100°,当∠AOC=30°时,∠BOD的度数是( )
A. 50° B. 80° C. 80°或150° D. 50°或110°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把正整数1,2,3,4,…排列成如图所示的一个表.
(1)用一正方形在表中随意框住4个数,把其中最大的数记为x,另三个数用含x的式子表示出来,从大到小依次是 , , ;
(2)在(1)的前提下,当被框住的4个数之和等于984时,x位于该表的第几行第几列?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,D是BC的中点,过D点的直线GF交AC于F,交AC的平行线BG于G点,DE⊥DF,交AB于点E,连结EG、EF.

(1)求证:BG=CF.
(2)请你判断BE+CF与EF的大小关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:一组数据x1,x2,x3,x4,x5的平均数是2,方差是![]() ,那么另一组数据3x1﹣2,3x2﹣2,3x3﹣2,3x4﹣2,3x5﹣2的平均数和方差分别是( )
,那么另一组数据3x1﹣2,3x2﹣2,3x3﹣2,3x4﹣2,3x5﹣2的平均数和方差分别是( )
A. 2,![]() B. 2,1 C. 4,
B. 2,1 C. 4,![]() D. 4,3
D. 4,3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂接受了20天内生产1200台GH型电子产品的总任务.已知每台GH型产品由4个G型装置和3个H型装置配套组成.工厂现有80名工人,每个工人每天能加工6个G型装置或3个H型装置.工厂将所有工人分成两组同时开始加工,每组分别加工一种装置,并要求每天加工的G、H型装置数量正好组成GH型产品.
(1)按照这样的生产方式,工厂每天能配套组成多少套GH型电子产品?
(2)工厂补充10名新工人,这些新工人只能独立进行G型装置的加工,且每人每天只能加工4个G型装置,则补充新工人后每天能配套生产多少产品?
(3)为了在规定期限内完成总任务,请问至少需要补充多少名(2)中的新工人才能在规定期内完成总任务?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,锐角三角形 ABC 和锐角三角形 A'B'C'中,AD、A'D'分别是边 BC、B'C'上的高,且AB=A'B',AD=A'D'.要使△ABC≌△A'B'C',则应补充条件:________(填写一个即可)
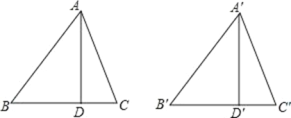
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上,点O为原点,点A表示的数为a,点B表示的数为b,且a,b满足![]()
![]() ,B两点对应的数分别为
,B两点对应的数分别为![]() ______,
______,![]() ______;
______;
![]() 若将数轴折叠,使得A点与B点重合,则原点O与数______表示的点重合;
若将数轴折叠,使得A点与B点重合,则原点O与数______表示的点重合;
![]() 若点A、B分别以4个单位
若点A、B分别以4个单位![]() 秒和3个单位
秒和3个单位![]() 秒的速度相向而行,则几秒后A、B两点相距1个单位长度?
秒的速度相向而行,则几秒后A、B两点相距1个单位长度?
![]() 若点A、B以
若点A、B以![]() 中的速度同时向右运动,点P从原点O以7个单位
中的速度同时向右运动,点P从原点O以7个单位![]() 秒的速度向右运动,是否存在常数m,使得
秒的速度向右运动,是否存在常数m,使得![]() 为定值,若存在,请求出m值以及这个定值;若不存在,请说明理由.
为定值,若存在,请求出m值以及这个定值;若不存在,请说明理由.
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com