
(本题12分)如图,过点A(0,3)的直线l1与x轴交于点B,tan∠ABO= .过点A的另一直线l2:y=-
.过点A的另一直线l2:y=- x+b (t>0)与x轴交于点Q,点P是射线AB上的一个动点,过P作PH⊥x轴于点H,设PB=5t.
x+b (t>0)与x轴交于点Q,点P是射线AB上的一个动点,过P作PH⊥x轴于点H,设PB=5t.

(1)求直线l1 的函数解析式;
(2)当点P在线段AB上运动时,设△PHQ的面积为S(S≠0),求S与t之间的函数关系式(要求写出自变量t的取值范围);
(3)当点P 在射线AB上运动时,是否存在这样的t值,使以P,H,Q为顶点的三角形与△AOQ相似?若存在,直接写出所有满足条件的t值所对应的P点坐标;若不存在,请说明理由.
(1)函数解析式为y=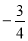 x+3;(2)①当H在Q、B之间时S=
x+3;(2)①当H在Q、B之间时S=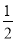 (4-8t)×3t=
(4-8t)×3t=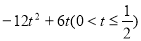 ②当H在O、Q之间时,S=
②当H在O、Q之间时,S=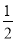 (8t-4) 3t=
(8t-4) 3t=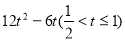 ;(3)t1=
;(3)t1=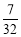 ,P1
,P1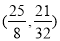 ;t2=
;t2=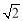 -1,P2
-1,P2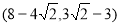 ; t3=
; t3=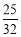 ,P3
,P3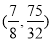 ;t4=1,P4(0,3);t5=1, P5(8,-3)
;t4=1,P4(0,3);t5=1, P5(8,-3)
【解析】
试题分析:(1)∵A(0,3),且tan∠ABO=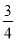 ∴B(4,0)
∴B(4,0)
设y=kx+b ,将A(0,3) B(4,0)代入上式得b=3 0=4k+b
解得k=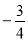 ,b=3
,b=3
∴ 函数解析式为y=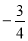 x+3
x+3
(2)由B(4,0).∴OB=4,
∵OA=3, ∴AB=5.
由题意,得△BHP∽△BOA,
∵OA∶OB∶AB=3∶4∶5,
∴HP∶HB∶BP=3∶4∶5,
∵PB=5t,∴HB=4t,HP=3t.
∴OH=OB-HB=4-4t.
由y=-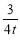 x+3与x轴交于点Q, 得Q(4t,0)
x+3与x轴交于点Q, 得Q(4t,0)
①当H在Q、B之间时(如图1)
QH=OH-OQ=(4-4t)-4t=4-8t.
S=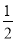 (4-8t)×3t=
(4-8t)×3t=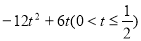
②当H在O、Q之间时(如图2)
QH=OQ-OH=4t-(4-4t)=8t-4.
S=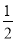 (8t-4) 3t=
(8t-4) 3t=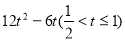
(3)存在t的值,使以P、H、Q为顶点的三角形与△AOQ相似
①当H在Q、B之间
t1=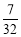 ,P1
,P1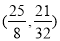 或者t2=
或者t2=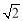 -1,P2
-1,P2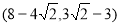
②当H在O、Q之间
t3=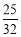 .得P3
.得P3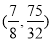 或者t4=1,P4(0,3)
或者t4=1,P4(0,3)
③当H在B的右侧
t5=1, P5(8,-3)


考点:一次函数的综合运用


科目:初中数学 来源:2013-2014学年浙江省宁波市九年级上学期第一次月考数学试卷(解析版) 题型:选择题
将抛物线y= (x -1)2 +3向左平移1个单位,再向下平移3个单位后所得抛物线的解析式为( )
A.y= (x -2)2 B.y= (x -2)2 +6 C.y=x2 +6 D.y=x2
查看答案和解析>>
科目:初中数学 来源:2013-2014学年浙江省宁波市九年级上学期期中考试数学试卷(解析版) 题型:选择题
设[x)表示大于x的最小整数,如[3)=4,[-1.2)=-1,则下列结论中正确的有( )
①[0)=0;
②[x)-x的最小值是0;
③[x)-x的最大值是0;
④存在实数x,使[x)-x=0.5成立.
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源:2013-2014学年浙江省宁波市九年级上学期期中考试数学试卷(解析版) 题型:选择题
下列图形中,阴影部分的面积相等的是( )

A、①② B、②③ C、③④ D、①④
查看答案和解析>>
科目:初中数学 来源:2013-2014学年浙江省丽水市莲都区九年级第一次中考模拟数学试卷(解析版) 题型:解答题
(本题6分)一艘中国海监船自西向东航行,在A处测得钓鱼岛C在海监船的北偏东68°方向,继续向东航行80海里到达B处,此时测得钓鱼岛C在海监船的北偏东26°方向上.问:海监船再继续向东航行多少海里,距离钓鱼岛C最近?(结果保留整数)(参考数据:sin68°≈0.93,cos68°≈0.37,tan68°≈2.48,sin26°≈0.44,cos26°≈0.90,tan26°≈0.49)

查看答案和解析>>
科目:初中数学 来源:2013-2014学年浙江省丽水市莲都区九年级第一次中考模拟数学试卷(解析版) 题型:填空题
某企业两年前创办时的资金为1000万元,现在已有资金1440万元.若设该企业这两年资金的年平均增长率为x,则根据题意可列方程为 ;
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省九年级直升班第一次综合测试数学试卷(解析版) 题型:解答题
如图所示, 是圆O的一条弦,
是圆O的一条弦,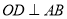 ,垂足为
,垂足为 ,交圆O于点
,交圆O于点 ,点
,点 在圆O上.
在圆O上.

(1)若 ,求
,求 的度数;
的度数;
(2)若AC=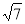 ,CD=1,求圆O的半径.
,CD=1,求圆O的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com