
【题目】如图,在Rt△ABC中,∠C=90°,AC=BC,AB=8,点D为AB的中点,若直角MDN绕点D旋转,分别交AC于点E,交BC于点F,则下列说法正确的有( ) ①AE=CF;②EC+CF=4 ![]() ;③DE=DF;④若△ECF的面积为一个定值,则EF的长也是一个定值.
;③DE=DF;④若△ECF的面积为一个定值,则EF的长也是一个定值.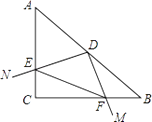
A.①②
B.①③
C.①②③
D.①②③④
【答案】D
【解析】解:①连接CD. 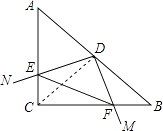
∵在Rt△ABC中,∠C=90°,AC=BC,点D为AB的中点,
∴CD⊥AB,CD=AD=DB,
在△ADE与△CDF中,∠A=DCF=45°,AD=CD,∠ADE=∠CDF,
∴△ADE≌△CDF,
∴AE=CF.说法正确;
②∵在Rt△ABC中,∠C=90°,AC=BC,AB=8,
∴AC=BC=4 ![]() .
.
由①知AE=CF,
∴EC+CF=EC+AE=AC=4 ![]() .说法正确;
.说法正确;
③由①知△ADE≌△CDF,
∴DE=DF.说法正确;
④∵△ECF的面积= ![]() ×CE×CF,如果这是一个定值,则CECF是一个定值,
×CE×CF,如果这是一个定值,则CECF是一个定值,
又∵EC+CF=4 ![]() ,
,
∴可唯一确定EC与EF的值,
再由勾股定理知EF的长也是一个定值,说法正确.
故选D.
【考点精析】认真审题,首先需要了解全等三角形的性质(全等三角形的对应边相等; 全等三角形的对应角相等),还要掌握勾股定理的概念(直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2)的相关知识才是答题的关键.


 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案科目:初中数学 来源: 题型:
【题目】如果将抛物线y=x2+2向下平移1个单位,那么所得新抛物线的表达式是( )
A.y=(x﹣1)2+2
B.y=(x+1)2+2
C.y=x2+1
D.y=x2+3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列各式: ![]() =
= ![]() =1﹣
=1﹣ ![]() ,
, ![]() =
= ![]() =
= ![]() ﹣
﹣ ![]() ,
, ![]() =
= ![]() =
= ![]() ﹣
﹣ ![]() ,
, ![]() =
= ![]() =
= ![]() ﹣
﹣ ![]() ,…
,…
(1)由此可推导出 ![]() =;
=;
(2)猜想出能表示上述特点的一般规律,用含字母n的等式表示出来(n是正整数);
(3)请用(2)中的规律计算 ![]() +
+ ![]() +…+
+…+ ![]() 的结果.
的结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,DE⊥BC,垂足为点E,连接AC交DE于点F,点G为AF的中点,∠ACD=2∠ACB.若DG=3,EC=1,则DE的长为( ) 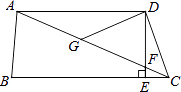
A.2 ![]()
B.![]()
C.2 ![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知下列四个命题:①两组邻边相等的四边形是平行四边形;②有三个角是直角的四边形是平行四边形;③有三个角相等的四边形是平行四边形;④一条对角线是另一条对角线的垂直平分线的四边形是平行四边形.其中真命题的个数是( )
A. 1 个B. 2 个C. 3 个D. 4 个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知双曲线y=![]() (k≠0)与正比例函数y=mx(m≠0)交于A、C两点,以AC为边作等边三角形ACD,且S△ACD=20
(k≠0)与正比例函数y=mx(m≠0)交于A、C两点,以AC为边作等边三角形ACD,且S△ACD=20![]() ,再以AC为斜边作直角三角形ABC,使AB∥y轴,连接BD.若△ABD的周长比△BCD的周长多4,则k的值是_______.
,再以AC为斜边作直角三角形ABC,使AB∥y轴,连接BD.若△ABD的周长比△BCD的周长多4,则k的值是_______.
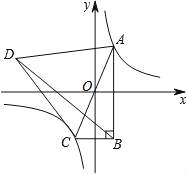
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com