
【题目】如图1,![]() 内接于
内接于![]() ,AD是直径,
,AD是直径,![]() 的平分线交BD于H,交
的平分线交BD于H,交![]() 于点C,连接DC并延长,交AB的延长线于点E.
于点C,连接DC并延长,交AB的延长线于点E.
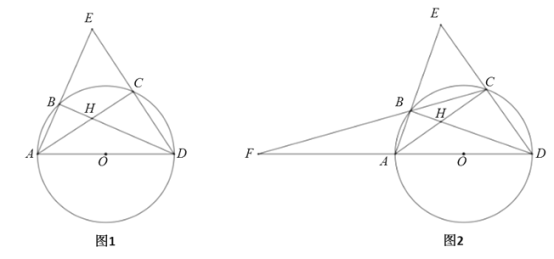
(1)求证:![]() ;
;
(2)若![]() ,求
,求![]() 的值
的值
(3)如图2,连接CB并延长,交DA的延长线于点F,若![]() ,求
,求![]() 的面积.
的面积.
【答案】(1)见解析;(2) ![]() ;(3)
;(3)![]()
【解析】
(1)根据直径所对的圆周角是直角可得![]() ,然后利用ASA判定△ACD≌△ACE即可推出AE=AD;
,然后利用ASA判定△ACD≌△ACE即可推出AE=AD;
(2)连接OC交BD于G,设![]() ,根据垂径定理的推论可得出OC垂直平分BD,进而推出OG为中位线,再判定
,根据垂径定理的推论可得出OC垂直平分BD,进而推出OG为中位线,再判定![]() ,利用对应边成比例即可求出
,利用对应边成比例即可求出![]() 的值;
的值;
(3)连接OC交BD于G,由(2)可知:OC∥AB,OG=![]() AB,然后利用ASA判定△BHA≌△GHC,设
AB,然后利用ASA判定△BHA≌△GHC,设![]() ,则
,则![]() ,再判定
,再判定![]() ,利用对应边成比例求出m的值,进而得到AB和AD的长,再用勾股定理求出BD,可求出△BED的面积,由C为DE的中点可得△BEC为△BED面积的一半,即可得出答案.
,利用对应边成比例求出m的值,进而得到AB和AD的长,再用勾股定理求出BD,可求出△BED的面积,由C为DE的中点可得△BEC为△BED面积的一半,即可得出答案.
(1)证明:∵AD是![]() 的直径
的直径
![]()
∵AC平分![]()
![]()
在△ACD和△ACE中,
∵∠ACD=∠ACE,AC=AC,∠DAC=∠EAC
∴△ACD≌△ACE(ASA)
![]()
(2)如图,连接OC交BD于G,
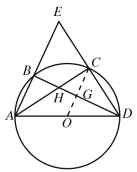
![]() ,设
,设![]() ,
,
则![]() ,OC=
,OC=![]() AD=
AD=![]()
![]()
![]()
∴OC垂直平分BD
又∵O为AD的中点
∴OG为△ABD的中位线
∴OC∥AB,OG=![]() ,CG=
,CG=![]()
![]()
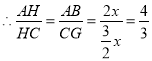
(3)如图,连接OC交BD于G,
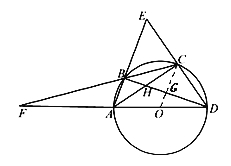
由(2)可知:OC∥AB,OG=![]() AB
AB
∴∠BHA=∠GCH
在△BHA和△GHC中,
∵∠BHA=∠GCH,AH=CH,∠BHA=∠GHC
![]()
∴![]()
设![]() ,则
,则![]()
又![]() ,
,
∴![]()
![]()
![]()
![]() ,
,
![]()
∵AD是![]() 的直径
的直径
![]()
![]()
![]()
又![]()
![]()
![]()


科目:初中数学 来源: 题型:
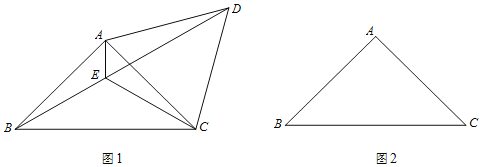
【题目】已知:在△ABC中,∠BAC=90°,AB=AC.
(1)如图1,将线段AC绕点A逆时针旋转60°得到AD,连结CD、BD,∠BAC的平分线交BD于点E,连结CE.
①求证:∠AED=∠CED;
②用等式表示线段AE、CE、BD之间的数量关系(直接写出结果);
(2)在图2中,若将线段AC绕点A顺时针旋转60°得到AD,连结CD、BD,∠BAC的平分线交BD的延长线于点E,连结CE.请补全图形,并用等式表示线段AE、CE、BD之间的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知y关于x的函数表达式是![]() ,下列结论不正确的是( )
,下列结论不正确的是( )
A.若![]() ,函数的最大值是5
,函数的最大值是5
B.若![]() ,当
,当![]() 时,y随x的增大而增大
时,y随x的增大而增大
C.无论a为何值时,函数图象一定经过点![]()
D.无论a为何值时,函数图象与x轴都有两个交点
查看答案和解析>>
科目:初中数学 来源: 题型:
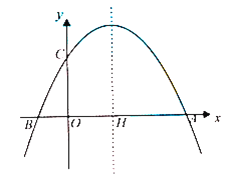
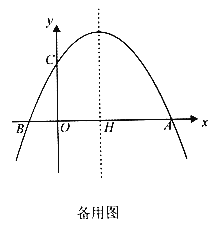
【题目】如图,在平面直角坐标系中,抛物线![]() 的图象与x轴交于
的图象与x轴交于![]() ,B两点,与y轴交于点
,B两点,与y轴交于点![]() ,对称轴
,对称轴![]() 与x轴交于点H.
与x轴交于点H.
(1)求抛物线的函数表达式
(2)直线![]() 与y轴交于点E,与抛物线交于点P,Q(点P在y轴左侧,点Q 在y轴右侧),连接CP,CQ,若
与y轴交于点E,与抛物线交于点P,Q(点P在y轴左侧,点Q 在y轴右侧),连接CP,CQ,若![]() 的面积为
的面积为![]() ,求点P,Q的坐标.
,求点P,Q的坐标.
(3)在(2)的条件下,连接AC交PQ于G,在对称轴上是否存在一点K,连接GK,将线段GK绕点G逆时针旋转90°,使点K恰好落在抛物线上,若存在,请直接写出点K的坐标不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
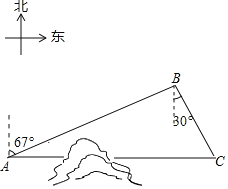
【题目】如图,C地在A地的正东方向,因有大山阻隔,由A地到C地需要绕行B地,已知B地位于A地北偏东67°方向,距离A地520km,C地位于B地南偏东30°方向,若打通穿山隧道,建成两地直达高铁,求A地到C地之间高铁线路的长(结果保留整数)(参考数据:sin67°≈0.92;cos67°≈0.38;![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
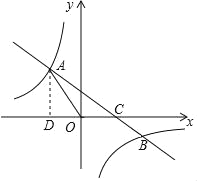
【题目】如图,在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象与反比例函数y=![]() (n≠0)的图象交于第二、四象限内的A、B两点,与x轴交于点C,点B 坐标为(m,﹣1),AD⊥x轴,且AD=3,tan∠AOD=
(n≠0)的图象交于第二、四象限内的A、B两点,与x轴交于点C,点B 坐标为(m,﹣1),AD⊥x轴,且AD=3,tan∠AOD=![]() .
.
(1)求该反比例函数和一次函数的解析式;
(2)求△AOB的面积;
(3)点E是x轴上一点,且△AOE是等腰三角形,请直接写出所有符合条件的E点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①是由五个完全相同的小正方体组成的立体图形,将图①中的一个小正方体改变位置后如图②.则三视图发生改变的是( )

A.主视图B.俯视图
C.左视图D.主视图、俯视图和左视图
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com