
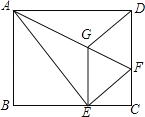
【题目】如图,将矩形ABCD沿AF折叠,使点D落在BC边的点E处,过点E作EG∥CD交AF于点G,连接DG.
(1)求证:四边形EFDG是菱形;
(2)探究线段EG、GF、AF之间的数量关系,并说明理由;
(3)若AG=6,EG=2![]() ,求BE的长.
,求BE的长.
【答案】(1)证明见解析;(2)EG2=![]() GFAF.理由见解析;(3)BE=
GFAF.理由见解析;(3)BE=![]() .
.
【解析】
(1)先依据翻折的性质和平行线的性质证明∠DGF=∠DFG,从而得到GD=DF,接下来依据翻折的性质可证明DG=GE=DF=EF;(2)连接DE,交AF于点O.由菱形的性质可知GF⊥DE,OG=OF=![]() GF,接下来,证明△DOF∽△ADF,由相似三角形的性质可证明DF2=FOAF,于是可得到GE、AF、FG的数量关系;(3)过点G作GH⊥DC,垂足为H.利用(2)的结论可求得FG=4,然后再△ADF中依据勾股定理可求得AD的长,然后再证明△FGH∽△FAD,利用相似三角形的性质可求得GH的长,最后依据BE=AD-GH求解即可.
GF,接下来,证明△DOF∽△ADF,由相似三角形的性质可证明DF2=FOAF,于是可得到GE、AF、FG的数量关系;(3)过点G作GH⊥DC,垂足为H.利用(2)的结论可求得FG=4,然后再△ADF中依据勾股定理可求得AD的长,然后再证明△FGH∽△FAD,利用相似三角形的性质可求得GH的长,最后依据BE=AD-GH求解即可.
(1)证明:∵GE∥DF,
∴∠EGF=∠DFG.
∵由翻折的性质可知:GD=GE,DF=EF,∠DGF=∠EGF,
∴∠DGF=∠DFG.
∴GD=DF.
∴DG=GE=DF=EF.
∴四边形EFDG为菱形.
(2)EG2=![]() GFAF.
GFAF.
理由:如图1所示:连接DE,交AF于点O.
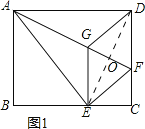
∵四边形EFDG为菱形,
∴GF⊥DE,OG=OF=![]() GF.
GF.
∵∠DOF=∠ADF=90°,∠OFD=∠DFA,
∴△DOF∽△ADF.
∴![]() ,即DF2=FOAF.
,即DF2=FOAF.
∵FO=![]() GF,DF=EG,
GF,DF=EG,
∴EG2=![]() GFAF.
GFAF.
(3)如图2所示:过点G作GH⊥DC,垂足为H.
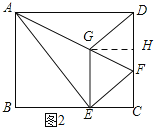
∵EG2=![]() GFAF,AG=6,EG=2
GFAF,AG=6,EG=2![]() ,
,
∴20=![]() FG(FG+6),整理得:FG2+6FG﹣40=0.
FG(FG+6),整理得:FG2+6FG﹣40=0.
解得:FG=4,FG=﹣10(舍去).
∵DF=GE=2![]() ,AF=10,
,AF=10,
∴AD=![]() =4
=4![]() .
.
GH⊥DC,AD⊥DC,
∴GH∥AD.
∴△FGH∽△FAD.
∴![]() ,即
,即![]() =
=![]() .
.
∴GH=![]() .
.
∴BE=AD﹣GH=4![]() ﹣
﹣![]() =
=![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】有两个一元二次方程M:ax2+bx+c=0,N:cx2+bx+a=0,其中a·c≠0,a≠c,下列四个结论:① 如果M有两个相等的实数根,那么N也有两个相等实数根;② 如果M与N有实数根,则M有一个根与N的一个根互为倒数;③ 如果M与N有实数根,且有一根相同,那么这个根必是1;④ 如果M的两根符号相同,那么N的两根符号也相同;其中正确的是( )
A.①②③B.①②④C.②③④D.①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=﹣x2+2x+3.
(1)求其开口方向、对称轴、顶点坐标,并画出这个函数的图象;
(2)根据图象,直接写出:①当函数值y为正数时,自变量x的取值范围;
②当﹣2<x<2时,函数值y的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有这样一道习题:如图1,已知OA和OB是⊙O的半径,并且OA⊥OB,P是OA上任一点(不与O、A重合),BP的延长线交⊙O于Q,过Q点作⊙O的切线交OA的延长线于R.说明:RP=RQ.请探究下列变化:
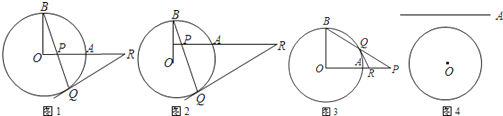
变化一:交换题设与结论.
已知:如图1,OA和OB是⊙O的半径,并且OA⊥OB,P是OA上任一点(不与O、A重合),BP的延长线交⊙O于Q,R是OA的延长线上一点,且RP=RQ.
求证:RQ为⊙O的切线.
变化二:运动探究:
(1)如图2,若OA向上平移,变化一中的结论还成立吗?(只需交待判断)
(2)如图3,如果P在OA的延长线上时,BP交⊙O于Q,过点Q作⊙O的切线交OA的延长线于R,原题中的结论还成立吗?为什么?
(3)若OA所在的直线向上平移且与⊙O无公共点,请你根据原题中的条件完成图4,并判断结论是否还成立?(只需交待判断)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了满足学生的个性化需求,新课程改革已经势在必行,某校积极开展拓展性课程建设,大体分为学科、文体、德育、其他等四个框架进行拓展课程设计。为了了解学生喜欢的拓展课程类型,学校随机抽取了部分学生进行调查,调查后将数据绘制成扇形统计图和条形统计图(未绘制完整).

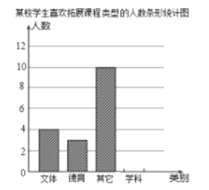
(1)求调查的学生总人数,并把条形图补充完整并填写扇形图中缺失的数据;
(2)小明同学说:“因为调查的同学中喜欢文体类拓展课程的同学占16%,而喜欢德育类拓展课程的同学仅占12%,所以全校2000名学生中,喜欢文体类拓展课程的同学人数一定比喜欢德育类拓展课程的同学人数多。”你觉得小明说得对吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某品牌牛奶供应商提供A,B,C,D四种不同口味的牛奶供学生饮用.某校为了了解学生对不同口味的牛奶的喜好,对全校订牛奶的学生进行了随机调查,并根据调查结果绘制了如下两幅不完整的统计图.根据统计图的信息解决下列问题:

(1)本次调查的学生有多少人?
(2)补全上面的条形统计图;
(3)扇形统计图中C对应的中心角度数是_____;
(4)若该校有600名学生订了该品牌的牛奶,每名学生每天只订一盒牛奶,要使学生能喝到自己喜欢的牛奶,则该牛奶供应商送往该校的牛奶中,A,B口味的牛奶共约多少盒?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x 的方程 x![]() 2m 1 x m
2m 1 x m![]() 2 0 。
2 0 。
(1)若方程总有两个实数根,求m 的取值范围;
(2)若两实数根![]() 、
、![]() 满足
满足 ![]() 1
1![]() 1 12 ,求 m 的值.
1 12 ,求 m 的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是矩形,AB=8,BC=4,动点P以每秒2个单位的速度从点A沿线段AB向B点运动,同时动点Q以每秒3个单位的速度从点B出发沿B-C-D的方向运动,当点Q到达点D时P、Q同时停止运动,若记△PQA的面积为y,运动时间为x,则下列图象中能大致表示y与x之间函数关系图象的是( )
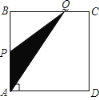
A.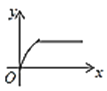 B.
B.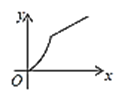 C.
C.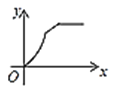 D.
D.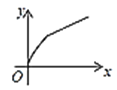
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=﹣![]() x+4与x轴、y轴分别交于点A、B、C是线段AB上一点,四边形OADC是菱形,则OD的长为( )
x+4与x轴、y轴分别交于点A、B、C是线段AB上一点,四边形OADC是菱形,则OD的长为( )
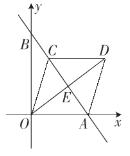
A. 4.2B. 4.8C. 5.4D. 6
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com