
����Ŀ��������һ��ϰ�⣺��ͼ1����֪OA��OB�ǡ�O�İ뾶������OA��OB��P��OA����һ�㣨����O��A�غϣ���BP���ӳ��߽���O��Q����Q������O�����߽�OA���ӳ�����R��˵����RP=RQ����̽�����б仯��
�仯һ��������������ۣ�
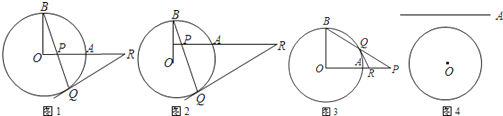
��֪����ͼ1��OA��OB�ǡ�O�İ뾶������OA��OB��P��OA����һ�㣨����O��A�غϣ���BP���ӳ��߽���O��Q��R��OA���ӳ�����һ�㣬��RP=RQ��
��֤��RQΪ��O�����ߣ�
�仯�����˶�̽����
��1����ͼ2����OA����ƽ�ƣ��仯һ�еĽ��ۻ������𣿣�ֻ�轻���жϣ�
��2����ͼ3�����P��OA���ӳ�����ʱ��BP����O��Q������Q����O�����߽�OA���ӳ�����R��ԭ���еĽ��ۻ�������Ϊʲô��
��3����OA���ڵ�ֱ������ƽ�������O�����㣬�������ԭ���е��������ͼ4�����жϽ����Ƿ�������ֻ�轻���жϣ�
���𰸡��仯һ�����������仯������1����OA����ƽ�ƣ��仯һ�еĽ��ۻ���������2��ԭ���еĽ��ۻ����������ɼ���������3��ԭ���еĽ��ۻ�����.
��������
ԭ�����֤��������OQ������RQΪ��O�����ߣ��ó���OQB+��PQR=90�������ݰ뾶OB=OQ��OA��OB���ó���OQB=��OBQ����OBQ+��BPO=90�����Ӷ��á�PQR=��QPR������ͬһ���������У��ȽǶԵȱߣ�֤������.
�仯һ��֤������ԭ�����֤�������෴����RP=RQ����֪��PQR=��QPR=��BPO����OB=OQ��OA��OB�ó���OQB=��OBQ����OBQ+��BPO=90���������û����ϵ���ǽ���ת����֤����OQB+��PQR=90��������OQR=90��������ɡ�OQR=90������֪RQΪ��O�����ߣ�
�仯����֤��������OQ������ԭ�����֤���������м���.
֤��������OQ��
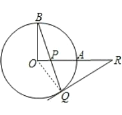
��RQΪ��O�����ߣ�
���OQR=��OQB+��PQR=90����
�֡�OB=OQ��OA��OB��
���OQB=��OBQ����OBQ+��BPO=90����
���PQR=��BPO��
����BPO=��QPR��
���PQR=��QPR��
��RP=RQ��
�仯һ��
֤������RP=RQ�����PQR=��QPR=��BPO��
�֡�OB=OQ��OA��OB��
���OQB=��OBQ����OBQ+��BPO=90����
���OQB+��PQR=90��������OQR=90����
��RQΪ��O�����ߣ�
�仯����
��1����OA����ƽ�ƣ��仯һ�еĽ��ۻ�������
��2��ԭ���еĽ��ۻ�������
���ɣ�����OQ��

��RQΪ��O�����ߣ�
���OQR=90������BQO+��RQP=90����
�֡�OB=OQ��OP��OB��
���OQB=��OBQ����OBQ+��BPO=90����
���RQP=��BPO��
��RP=RQ��
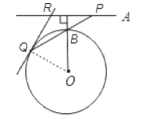
��3��ԭ���еĽ��ۻ���������ͼ��


 Ӯ�ڿ�����ʦ��ʱ�ƻ�ϵ�д�
Ӯ�ڿ�����ʦ��ʱ�ƻ�ϵ�д� �������Ͽ�ʱͬ��ѵ��ϵ�д�
�������Ͽ�ʱͬ��ѵ��ϵ�д� �������ͬ����ϰϵ�д�
�������ͬ����ϰϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У�һ�κ�����ͼ����A(2��3)���B(0��5)��
��1�����һ�κ����Ľ���ʽ��
��2����P��Ϊ��һ�κ���ͼ����һ�㣬�ҡ�POB�����Ϊ10.���P���ꡣ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=ax2+bx+c��a��0���Ķ������������y��Ľ�����һ�κ���y=kx+1��k��0����ͼ���ϣ����ĶԳ�����x=1���������ĸ����ۣ���abc��0����a����![]() ����a=��k���ܵ�0��x��1ʱ��ax+b��k��������ȷ���۵ĸ����ǣ�������
����a=��k���ܵ�0��x��1ʱ��ax+b��k��������ȷ���۵ĸ����ǣ�������

A. 4 B. 3 C. 2 D. 1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��ABC�У�AB��AC���ѡ�ABC��A����˳ʱ�뷽����ת�õ���ADE������BD��CE���ڵ�F��

��1����֤����AEC�ա�ADB����2����AB��2����BAC��45�㣬���ı���ADFC������ʱ����BF�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ͼ������O�У�AB��CD��ֱ����BE�����ߣ�BΪ�е㣬
����AD��BC��BD��
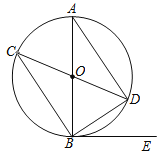
��1����֤����ABD�ա�CDB��
��2������DBE=35�㣬����ADC�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У�������y��ax2+bx+c��x�ύ��A��1��0����B��3��0������y�ύ��C��0��3���������߶���ΪD�㣮
(1)��������߽���ʽ��
(2)��ͼ1����PΪ�������ϵ�һ�����㣬���ڶԳ����Ҳ࣬����ADP���Ϊ3�����P�����ꣻ
(3)��(2)�������£�PA���Գ����ڵ�E����ͼ2����E�����һ��ֱ���������߽���M��N���㣬ֱ��MD��ֱ��y����3�ڵ�F������NF����֤��NF��y�ᣮ
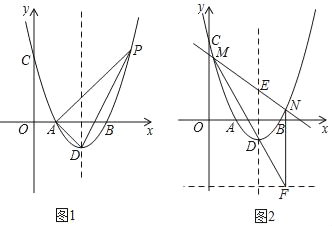
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD��AF�۵���ʹ��D����BC�ߵĵ�E��������E��EG��CD��AF�ڵ�G������DG��
��1����֤���ı���EFDG�����Σ�
��2��̽���߶�EG��GF��AF֮���������ϵ����˵�����ɣ�
��3����AG=6��EG=2![]() ����BE�ij���
����BE�ij���
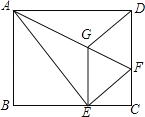
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������![]() ��һԪ���η���
��һԪ���η���![]() .
.
��1����֤��������������ʵ������
��2����������һ��С��1����![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˽�ij��ѧѧ�����������ڼ��Լ�����������˷��������IJ��������Сǿ��ȫУ��Χ�������ȡ��������ѧ������ij���緹�˷ѷ�����������˵��飬���������ݷ�Ϊ���飺![]() ���Ͳ�ȫ�����ꣻ
���Ͳ�ȫ�����ꣻ![]() ����ʣ�����˳��ꣻ
����ʣ�����˳��ꣻ![]() �������굫����ʣ��
�������굫����ʣ��![]() �����Ͳ˶���ʣ.���ݵ���������������ͼ��ʾ������������ͳ��ͼ.
�����Ͳ˶���ʣ.���ݵ���������������ͼ��ʾ������������ͳ��ͼ.

�ش��������⣺
��1����α�����ѧ������ �ˣ�����ͳ��ͼ�У���![]() ��������Ӧ��Բ�ĽǵĶ���Ϊ ��
��������Ӧ��Բ�ĽǵĶ���Ϊ ��
��2����ȫ����ͳ��ͼ��
��3����֪����ѧ����ѧ��![]() �ˣ�����������緹��ʣ����ѧ������������ƽ��ÿ��ʣ
�ˣ�����������緹��ʣ����ѧ������������ƽ��ÿ��ʣ![]() �������㣬�����緹���˷Ѷ���ǧ������
�������㣬�����緹���˷Ѷ���ǧ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com