
分析 (1)首先分别计算出两个不等式的解集,再根据大小小大中间找确定不等式组的解集;
(2)首先两边同时乘以x2-9去分母,然后再整理成一元一次方程,再解即可,注意不要忘记检验.
解答 解:(1)$\left\{\begin{array}{l}{2(2x-1)≤3x+4①}\\{\frac{2x-1}{3}-\frac{5x+1}{2}≤1②}\end{array}\right.$,
由①得:x≤6,
由②得:x≥-1,
画图:
所以原不等式组的解集为-1≤x≤6;
(2)两边同乘以x2-9,得:
3+x(x+3)=x2-9,
化简,得3x=-12,
解得:x=-4,
经检验,x=-4是原方程的根.
点评 此题主要考查了解一元一次不等式组,以及分式方程,关键是掌握解集的规律:同大取大;同小取小;大小小大中间找;大大小小找不到.


 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
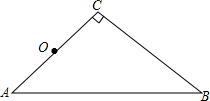 在等腰直角三角形ABC中,∠C=90°,BC=2cm.以AC的中点O为对称中心,画出与△ABC关于点O成中心对称的△DEF,点A、B、C的对称点分别是点D、E、F,并求出BE的长.
在等腰直角三角形ABC中,∠C=90°,BC=2cm.以AC的中点O为对称中心,画出与△ABC关于点O成中心对称的△DEF,点A、B、C的对称点分别是点D、E、F,并求出BE的长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
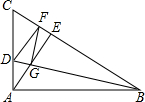 在△ABC中,∠BAC=90°,在BC上截取BF=AB,DF⊥BC交AC于点D,连接BD交BC边的高AE于G,连接GF,则∠AGD与∠FGD有什么关系?试说明理由.
在△ABC中,∠BAC=90°,在BC上截取BF=AB,DF⊥BC交AC于点D,连接BD交BC边的高AE于G,连接GF,则∠AGD与∠FGD有什么关系?试说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com