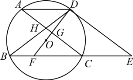
【题目】如图，⊙O的弦AD∥BC，过点D的切线交BC的延长线于点E，AC∥DE交BD于点H，DO及其延长线分别交AC，BC于点G，F.
（1）求证：DF垂直平分AC；
（2）若弦AD=10，AC=16，求⊙O的半径.
【答案】（1）见解析；（2）⊙O的半径为
.
【解析】
（1）根据“切线的性质和垂径定理”进行分析证明即可；
（2）如下图，连接AO，由垂径定理可得AG=
AC=8，这样在Rt△ADG中由勾股定理可得GD=6，设⊙O的半径为r，则OG=r-6，由此在Rt△AOG中由勾股定理建立关于r的方程，解方程即可求得r的值.
（1）∵DE是⊙O的切线，且DF过圆心O，
∴DF⊥DE.
又∵AC∥DE，∴DF垂直平分AC.
（2）如下图，连接AO，
∵AG=GC，AC=16，
∴AG=8.
∴在Rt△AGD中，GD=
，
设⊙O的半径为r，则OG=r-6，
∵ 在Rt△AOG中，
，
∴
.
解得r=.即⊙O的半径为.
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，AD⊥BC，EF垂直平分AC，交AC于点F，交BC于点E，且BD=DE．
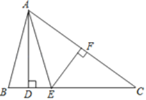
（1）若∠C=40°，求∠BAD的度数；
（2）若AC=5，DC=4，求△ABC的周长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（1）因式分解：-28m3n2+42m2n3-14m2n
（2）因式分解：9a2（x-y）+4b2（y-x）
（3）求不等式
的负整数解
（4）解不等式组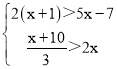
，把它们的解集在数轴上表示出来．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某中学九年级甲、乙两班分别选5名同学参加“奋发向上，崇德向善”演讲比赛,其预赛成绩如图所示:
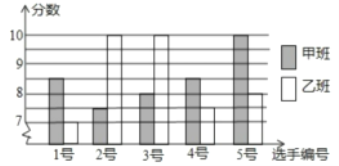
(1)根据上图填写下表:
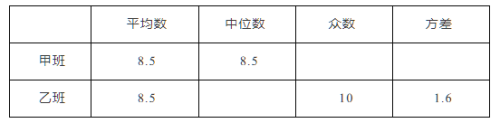
(2)根据上表数据，分别从平均数、中位数、众数、方差的角度分析哪班的成绩较好.
查看答案和解析>>
科目：初中数学 来源： 题型：
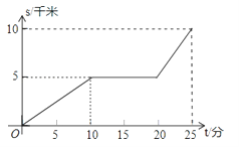
【题目】某天早晨，王老师从家出发，骑摩托车前往学校，途中在路旁一家饭店吃早餐，如图所示的是王老师从家到学校这一过程中行驶路程s（千米）与时间t（分）之间的关系．
（1）学校离他家多远？从出发到学校，用了多少时间？
（2）王老师吃早餐用了多少时间？
（3）王老师吃早餐以前的速度快还是吃完早餐以后的速度快？最快时速达到多少？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】正方形A1B1C1O，A2B2C2C1，A3B3C3C2，…按如图的方式放置．点A1，A2，A3，…和点C1，C2，C3，…分别在直线y=x+1和x轴上，则点A6的坐标是（ ）
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：初中数学 来源： 题型：
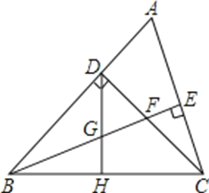
【题目】已知：如图，△ABC中，∠ABC＝45°，CD⊥AB于D，BE平分∠ABC，且BE⊥AC于E，与CD相交于点F，H是BC边的中点，连结DH与BE相交于点G．
（1）求证：BF＝AC；
（2）求证：CE＝
BF．
查看答案和解析>>
科目：初中数学 来源： 题型：
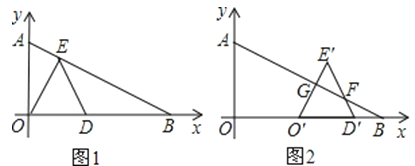
【题目】在Rt△ABO中，∠AOB=90°，OA=
，OB=4，分别以OA、OB边所在的直线建立平面直角坐标系，D为x轴正半轴上一点，以OD为一边在第一象限内作等边△ODE．
（1）如图①，当E点恰好落在线段AB上时，求E点坐标；
（2）在（Ⅰ）问的条件下，将△ODE沿x轴的正半轴向右平移得到△O′D′E′，O′E′、D′E′分别交AB于点G、F（如图②）求证OO′=E′F；
（3）若点D沿x轴正半轴向右移动，设点D到原点的距离为x，△ODE与△AOB重叠部分的面积为y，请直接写出y与x的函数关系式．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
