
| A�� | 35 | B�� | 350 | C�� | 840 | D�� | 2520 |
 �������Ӧ���⼯ѵϵ�д�
�������Ӧ���⼯ѵϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��a2b��3=a6b3 | B�� | a6��a2=a3��a��0�� | C�� | a-2=-$\frac{1}{{a}^{2}}$��a��0�� | D�� | $\root{3}{��-2��^{3}}$=2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 5 cm | B�� | 10 cm | C�� | 15 cm | D�� | 30 cm |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
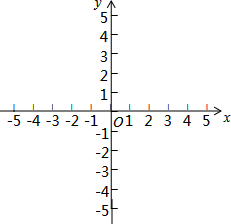 �����Ա���x�IJ�ͬ��ȡֵ��Χ�����Ų�ͬ�Ķ�Ӧ���������ĺ���ͨ�������ֶκ���������һ�������������Ǽ����������ֶκ����ڲ�ͬ�Ķ������ϣ������ı���ʽҲ��ͬ�����磺y=$\left\{\begin{array}{l}{{x}^{2}-2x��x��0��}\\{2x��x��0��}\end{array}\right.$�Ƿֶκ�������x��0ʱ�����Ƕ��κ���y=x2-2x����x��0ʱ����������������y=2x��
�����Ա���x�IJ�ͬ��ȡֵ��Χ�����Ų�ͬ�Ķ�Ӧ���������ĺ���ͨ�������ֶκ���������һ�������������Ǽ����������ֶκ����ڲ�ͬ�Ķ������ϣ������ı���ʽҲ��ͬ�����磺y=$\left\{\begin{array}{l}{{x}^{2}-2x��x��0��}\\{2x��x��0��}\end{array}\right.$�Ƿֶκ�������x��0ʱ�����Ƕ��κ���y=x2-2x����x��0ʱ����������������y=2x���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��AE��AB����AE=AB��BC��CD����BC=CD���밴��ͼ������ע�����ݼ���ͼ��ʵ����Χ�ɵ�ͼ�ε����S=50��
��ͼ��AE��AB����AE=AB��BC��CD����BC=CD���밴��ͼ������ע�����ݼ���ͼ��ʵ����Χ�ɵ�ͼ�ε����S=50���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
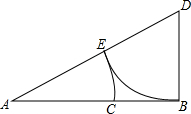 ��ͼ���߶�AB=2������B��BD��AB��ʹBD=$\frac{1}{2}$AB������AD����AD�Ͻ�ȡDE=DB����AB�Ͻ�ȡAC=AE����ô�߶�AC�ij�Ϊ$\sqrt{5}$-1��
��ͼ���߶�AB=2������B��BD��AB��ʹBD=$\frac{1}{2}$AB������AD����AD�Ͻ�ȡDE=DB����AB�Ͻ�ȡAC=AE����ô�߶�AC�ij�Ϊ$\sqrt{5}$-1���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com