
分析 因为一个数的算术平方根是非负数,先由非负数的和等于0,求出a、b的值,把a、b代入并求出$\sqrt{{a}^{2}+{b}^{2}+7}$的值.
解答 解:∵$\sqrt{a-\sqrt{5}-2}$≥0,$\sqrt{b-\sqrt{5}+2}$≥0,
又∵$\sqrt{a-\sqrt{5}-2}$+$\sqrt{b-\sqrt{5}+2}$=0,
∴a-$\sqrt{5}-2=0$,b-$\sqrt{5}$+2=0,
即a=$\sqrt{5}+2$,b=$\sqrt{5}$-2
∴a2+b2+7=($\sqrt{5}+2$)2+($\sqrt{5}$-2)2+7
=5+4$\sqrt{5}$+4+5-4$\sqrt{5}$+4+7
=25
∴$\sqrt{{a}^{2}+{b}^{2}+7}$
=$\sqrt{25}$
=5.
点评 本题考查了非负数的算式平方根和二次根式的化简.解决本题的关键是根据非负数的和为零求出a、b的值.初中阶段学过的非负数有:一个数的绝对值、一个数的偶次方、一个数的算术平方根.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
| A. | 35 | B. | 350 | C. | 840 | D. | 2520 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
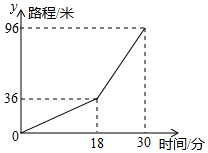 小亮早晨从家骑车到学校,先上坡后下坡,行程情况如图所示.
小亮早晨从家骑车到学校,先上坡后下坡,行程情况如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | -1 | C. | 2 | D. | $\frac{5}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
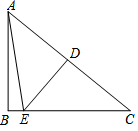 如图,在Rt△ABC中,∠B为直角,DE是AC的垂直平分线,DE交AC于点D,交BC于点E,且∠BAE:∠BAC=1:5,则∠C=40°.
如图,在Rt△ABC中,∠B为直角,DE是AC的垂直平分线,DE交AC于点D,交BC于点E,且∠BAE:∠BAC=1:5,则∠C=40°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com