
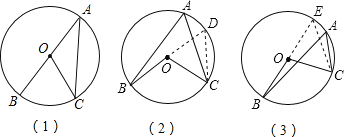
【题目】证明:同弧所对的圆周角等于它所对圆心角度数的一半.
【答案】证明见解析.
【解析】
根据圆心的位置分三种情形分别证明即可.
证明:①如图(1),当点O在∠BAC的一边上时,
∵OA=OC,
∴∠A=∠C,
∵∠BOC=∠A+∠C,
∴∠BAC=![]() ∠BOC;
∠BOC;
②如图(2)当圆心O在∠BAC的内部时,延长BO交⊙O于点D,连接CD,则
∠D=∠A(同弧或等弧所对的圆周角都相等),
∵OC=OD,
∴∠D=∠OCD,
∵∠BOC=∠D+∠OCD(三角形的一个外角等于与它不相等的两个内角的和),
∴∠BOC=2∠A,
即∠BAC=![]() ∠BOC.
∠BOC.
③如图(3),当圆心O在∠BAC的外部时,延长BO交⊙O于点E,连接CE,则
∠E=∠A(同弧或等弧所对的圆周角都相等),
∵OC=OE,
∴∠E=∠OCE,
∵∠BOC=∠E+∠OCE(三角形的一个外角等于与它不相邻的两个内角的和),
∴∠BOC=2∠A,
即∠BAC=![]() ∠BOC.
∠BOC.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+b x+c经过A,B,C三点,当x≥0时,其图象如图所示.
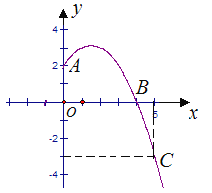
(1)求抛物线的解析式,写出抛物线的顶点坐标;
(2)画出抛物线y=ax2+b x+c当x<0时的图象;
(3)利用抛物线y=ax2+b x+c,写出x为何值时,y>0.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=ax2+2ax﹣3a(a>0)与x轴交于A,B两点(点A在点B的左侧).
(1)求抛物线的对称轴及线段AB的长;
(2)抛物线的顶点为P,若∠APB=120°,求顶点P的坐标及a的值;
(3)若在抛物线上存在一点N,使得∠ANB=90°,结合图象,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】蜂蜜具有消食、润肺、安神、美颜之功效,是天然的健康保健佳品.秋天即将来临时,雪宝山土特产公司抓住商机购进甲、乙、丙三种蜂蜜,已知销售每瓶甲蜂蜜的利润率为10%,每瓶乙蜂蜜的利润率为20%,每瓶丙蜂蜜的利润率为30%.当售出的甲、乙、丙蜂蜜瓶数之比为1:3:1时,商人得到的总利润率为22%;当售出的甲、乙、丙蜂蜜瓶数之比为3:2:1时,商人得到的总利润率为20%.那么当售出的甲、乙、丙蜂蜜瓶数之比为5:6:1时,该公司得到的总利润率为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,⊙M与y轴相切于原点O,平行于x轴的直线交⊙M于P、Q两点,点P在点Q的右边,若P点的坐标为(-1,2),则Q点的坐标是

A. (-4,2) B. (-4.5,2) C. (-5,2) D. (-5.5,2 )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某网店销售一种儿童玩具,进价为每件30元,物价部门规定每件儿童玩具的销售利润不高于进价的![]() .在销售过程中发现,这种儿童玩具每天的销售量
.在销售过程中发现,这种儿童玩具每天的销售量![]() (件
(件![]() 与销售单价
与销售单价![]() (元
(元![]() 满足一次函数关系.当销售单价为35元时,每天的销售量为350件;当销售单价为40元时,每天的销售量为300件.
满足一次函数关系.当销售单价为35元时,每天的销售量为350件;当销售单价为40元时,每天的销售量为300件.
(1)求![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
(2)当销售单价为多少时,该网店销售这种儿童玩具每天获得的利润最大,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是圆O的直径,点C在BA的延长线上,直线CD与圆O相切于点D,弦DF⊥AB于点E,连接BD,CD=BD=4![]() ,则OE的长度为( )
,则OE的长度为( )
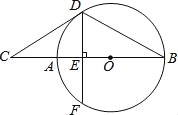
A.![]() B.2C.2
B.2C.2![]() D.4
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形ABCD中,E,F分别是AB,AD边上的点,DE与CF交于点G.
(1)如图①,若四边形ABCD是矩形,且DE⊥CF,求证:![]() ;
;
(2)如图②,若四边形ABCD是平行四边形,试探究:当∠B与∠EGC满足什么关系时,使得![]() 成立?并证明你的结论.
成立?并证明你的结论.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com