
【题目】已知四边形ABCD中,E,F分别是AB,AD边上的点,DE与CF交于点G.
(1)如图①,若四边形ABCD是矩形,且DE⊥CF,求证:![]() ;
;
(2)如图②,若四边形ABCD是平行四边形,试探究:当∠B与∠EGC满足什么关系时,使得![]() 成立?并证明你的结论.
成立?并证明你的结论.

【答案】(1)详见解析;(2)当∠B+∠EGC=180°时,![]() 成立,理由详见解析.
成立,理由详见解析.
【解析】
(1)根据矩形的性质可得∠A=∠ADC=90°,由DE⊥CF可得∠ADE=∠DCF,即可证得△ADE∽△DCF,从而证得结论;
(2)在AD的延长线上取点M,使CM=CF,则∠CMF=∠CFM.根据平行线的性质可得∠A=∠CDM,再结合∠B+∠EGC=180°,可得∠AED=∠FCB,进而得出∠CMF=∠AED即可证得△ADE∽△DCM,从而证得结论;
解:(1)∵四边形ABCD是矩形,∴∠A=∠ADC=90°,
∵DE⊥CF,∴∠ADE=∠DCF,
∴△ADE∽△DCF,
∴![]()
(2)当∠B+∠EGC=180°时,![]() 成立,证明如下:
成立,证明如下:
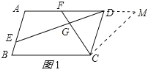
在AD的延长线上取点M,使CM=CF,
则∠CMF=∠CFM.
∵AB∥CD.∴∠A=∠CDM.
∵AD∥BC,∴∠CFM=∠FCB.
∵∠B+∠EGC=180°,∴∠AED=∠FCB,
∴∠CMF=∠AED,∴△ADE∽△DCM,∴![]() ,即
,即![]() .
.


科目:初中数学 来源: 题型:
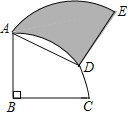
【题目】如图,将半径为4,圆心角为90°的扇形BAC绕A点逆时针旋转60°,点B、C的对应点分别为点D、E且点D刚好在![]() 上,则阴影部分的面积为_____.
上,则阴影部分的面积为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有长为24m的篱笆,一面利用墙(墙的最大可用长度a为10m),围成中间隔有一道篱笆的长方形花圃.设花圃的宽AB为xm,面积为Sm2.
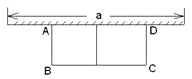
(1)求S与x的函数关系式;
(2)如果要围成面积为45m2的花圃,AB的长是多少米?
(3)能围成面积比45 m2更大的花圃吗?如果能,请求出最大面积,并说明围法;如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
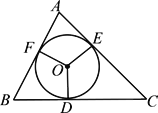
【题目】如图,△ABC的内切圆⊙O与BC,CA,AB分别相切于点D,E,F,且AB=9 cm,BC=14 cm,CA=13 cm,则AF的长为 __________
查看答案和解析>>
科目:初中数学 来源: 题型:
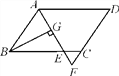
【题目】如图,在平行四边形ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE于点G,BG=4![]() ,则△EFC的周长为( )
,则△EFC的周长为( )
A. 11 B. 10 C. 9 D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
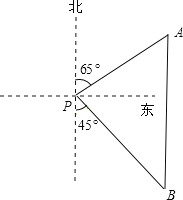
【题目】如图,一艘海轮位于灯塔P的北偏东65°方向,距离灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向上的B处,这时,海轮所在的B处距离灯塔P有多远?(结果用非特殊角的三角函数及根式表示即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】广安市某楼盘准备以每平方米6000元的均价对外销售,由于国务院有关房地产的新政策出台后,购房者持币观望,房地产开发商为了加快资金周转,对价格经过两次下调后,决定以每平方米4860元的均价开盘销售.
(1)求平均每次下调的百分率.
(2)某人准备以开盘价均价购买一套100平方米的住房,开发商给予以下两种优惠方案以供选择:①打9.8折销售;②不打折,一次性送装修费每平方米80元,试问哪种方案更优惠?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一条长为56cm的铁丝剪成两段并把每一段铁丝做成一个正方形.
(1)要使这两个正方形的面积之和等于100cm2,该怎么剪?
(2)设这两个正方形的面积之和为Scm2,当两段铁丝长度分别为何值时,S有最小值?
查看答案和解析>>
科目:初中数学 来源: 题型:
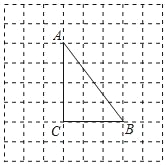
【题目】如图,将△ABC放在每个小正方形的边长为1的网格中,点A,点B,点C均落在格点上.(1)计算AB的长等于__,(2)请在如图所示的网格中,用无刻度的直尺,画出一个△ADE,使△ADE~△ABC,且满足点D在AC边上,点E在AB边上,AE=2.简要说明画图方法(不要求证明)__.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com