Question

19．如图：已知等边△ABC中，D是AC的中点，E是BC延长线上的一点，且CE=CD，DM⊥BC，垂足为M，
（1）求证：M是BE的中点．
（2）若等边三角形的边长为4，请求出DE的长．

Answer 1

分析 （1）要证M是BE的中点，根据题意可知，证明△BDE△为等腰三角形，利用等腰三角形的高和中线向重合即可得证；
（2）先根据等边三角形的性质求出BD的长，再判断出△BDE是等腰三角形即可．

解答 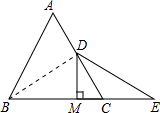解：（1）证明：连接BD，
∵在等边△ABC，且D是AC的中点，
∴∠DBC=$\frac{1}{2}$∠ABC=$\frac{1}{2}$×60°=30°，∠ACB=60°，
∵CE=CD，
∴∠CDE=∠E，
∵∠ACB=∠CDE+∠E，
∴∠E=30°，
∴∠DBC=∠E=30°，
∴BD=ED，△BDE为等腰三角形，
又∵DM⊥BC，
∴M是BE的中点；
（2）∵△ABC是边长为4的等边三角形，BD是AC边上的中线，
∴∠ACB=60°，BD⊥AC，BD平分∠ABC，∠DBE=$\frac{1}{2}$∠ABC=30°，
∴BD=BC•sin60°=4×$\frac{\sqrt{3}}{2}$=2$\sqrt{3}$．

点评 本题考查了等腰三角形顶角平分线、底边上的中线和高三线合一的性质以及等边三角形每个内角为60°的知识．辅助线的作出是正确解答本题的关键