
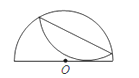
【题目】一张半径为2的半圆图纸沿它的一条弦折叠,使其弧与直径相切,如图所示,O为半圆圆心,如果切点分直径之比为3:1,则折痕长为( )
A. 3 B. ![]() C.
C. ![]() D. 2
D. 2![]()
【答案】C
【解析】
过O作弦BC的垂线OP,垂足为D,分别与弧的交点为A、G,过切点F作PF⊥半径OE交OP于P点,根据垂径定理及其推论得到BD=DC,即OP为BC的中垂线,OP必过弧BGC所在圆的圆心,再根据切线的性质得到PF必过弧BGC所在圆的圆心,则点P为弧BGC所在圆的圆心,根据折叠的性质有⊙P为半径等于⊙O的半径,即PF=PG=OE=2,并且AD=GD,由F点分⊙O的直径为3:1两部分可计算出OF=1,在Rt△OPF中,设OG=x,利用勾股定理可计算出x,则由AG=PG-AP计算出AG,可得到DG的长,于是可计算出OD的长,在Rt△OBD中,利用勾股定理计算BD,即可得到BC的长.
过O作弦BC的垂线OP,垂足为D,分别与弧的交点为A、G,过切点F作PF⊥半径OE交OP于P点,如图,
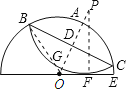
∵OP⊥BC,
∴BD=DC,即OP为BC的中垂线,
∴OP必过弧BGC所在圆的圆心,
又∵OE为弧BGC所在圆的切线,PF⊥OE,
∴PF必过弧BGC所在圆的圆心,
∴点P为弧BGC所在圆的圆心,
∵弧BAC沿BC折叠得到弧BGC,
∴⊙P为半径等于⊙O的半径,即PF=PG=OE=2,并且AD=GD,
∴OG=AP,
而F点分⊙O的直径为3:1两部分,
∴OF=1,
在Rt△OPF中,设OG=x,则OP=x+2,
∴OP2=OF2+PF2,即(x+2)2=12+22,解得x=![]() -2,
-2,
∴AG=2-(![]() -2)=4-
-2)=4-![]() ,
,
∴DG=![]() ,
,
∴OD=OG+DG=![]() -2+2-
-2+2-![]() =
=![]() ,
,
在Rt△OBD中,BD2=OB2+OD2,即BD2=22-(![]() )2,
)2,
∴BD=![]() ,
,
∴BC=2BD=![]() .
.
故选C.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:初中数学 来源: 题型:
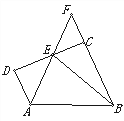
【题目】如图,梯形ABCD中,AD∥BC,∠D=90°,BC=CD=12,∠ABE=45°,点E在DC上,AE,BC的延长线相交于点F,若AE=10,则S△ADE+S△CEF的值是______ .
查看答案和解析>>
科目:初中数学 来源: 题型:
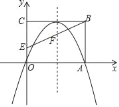
【题目】如图,在平面直角坐标系中,矩形OABC的顶点A、C分别在x轴、y轴的正半轴上,且OA=4,OC=3,若抛物线经过O,A两点,且顶点在BC边上,点E的坐标分别为(0,1),对称轴交BE于点F.
(1)求该抛物线的表达式;
(2)点M在对称轴右侧的抛物线上,点N在x轴上,请问是否存在以点A,F,M,N为顶点的四边形是平行四边形?若存在,请求出所有符合条件的点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
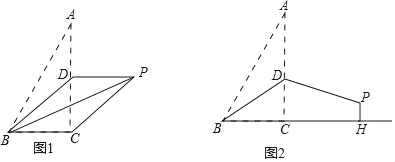
【题目】已知,在Rt△ABC中,∠ACB=90°,BC=4,AB=4![]() ,点D是AC边上的一个动点,将△ABD沿BD所在直线折叠,使点A落在P处.
,点D是AC边上的一个动点,将△ABD沿BD所在直线折叠,使点A落在P处.
(1)如图1,若点D是AC中点,连接PC.
①求AC的长;
②试猜想四边形BCPD的形状,并加以证明;
(2)如图2,若BD=AD,过点P作PH⊥BC交BC的延长线于点H,求CH的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
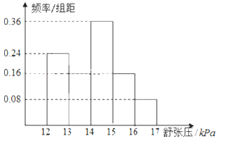
【题目】为了研究某药品的疗效,现选取若干名志愿者进行临床试验.所有志愿者的舒张压数据(单位:kPa)的分组区间为[12,13),[13,14),[14,15),[15,16),[16,17],将其按从左到右的顺序分别编号为第一组、第二组、…、第五组.如图是根据试验数据制成的频率分布直方图.
(1)若第一组接受治疗的志愿者有12人,则第三组接受治疗的志愿者有多少人?
(2)若接受治疗的志愿者共有50人,规定舒张压在14kpa以上的志愿者接受进一步的临床试验,若从三组志愿者中按比例分配20张床位,则舒张压数据在[14,15)的志愿者总共可以得到多少张床位?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=x2+bx+c经过A(﹣1,0)、B(3,0)两点.
(1)请求出抛物线的解析式;
(2)当0<x<4时,请直接写出y的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商家销售一款商品,进价每件80元,售价每件145元,每天销售40件,每销售一件需支付给商场管理费5元,未来一个月![]() 按30天计算
按30天计算![]() ,这款商品将开展“每天降价1元”的促销活动,即从第一天开始每天的单价均比前一天降低1元,通过市场调查发现,该商品单价每降1元,每天销售量增加2件,设第x天
,这款商品将开展“每天降价1元”的促销活动,即从第一天开始每天的单价均比前一天降低1元,通过市场调查发现,该商品单价每降1元,每天销售量增加2件,设第x天![]() 且x为整数
且x为整数![]() 的销售量为y件.
的销售量为y件.
![]() 直接写出y与x的函数关系式;
直接写出y与x的函数关系式;
![]() 设第x天的利润为w元,试求出w与x之间的函数关系式,并求出哪一天的利润最大?最大利润是多少元?
设第x天的利润为w元,试求出w与x之间的函数关系式,并求出哪一天的利润最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, 四边形OABC为直角梯形,A(4,0),B(3,4),C(0,4). 点![]() 从
从![]() 出发以每秒2个单位长度的速度向
出发以每秒2个单位长度的速度向![]() 运动;点
运动;点![]() 从
从![]() 同时出发,以每秒1个单位长度的速度向
同时出发,以每秒1个单位长度的速度向![]() 运动.其中一个动点到达终点时,另一个动点也随之停止运动.过点
运动.其中一个动点到达终点时,另一个动点也随之停止运动.过点![]() 作
作![]() 垂直
垂直![]() 轴于点
轴于点![]() ,连结AC交NP于Q,连结MQ.
,连结AC交NP于Q,连结MQ.
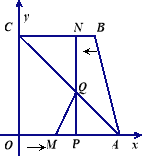
【1】点 (填M或N)能到达终点;
【1】求△AQM的面积S与运动时间t的函数关系式,并写出自变量t的取值范围,当t为何值时,S的值最大;
【1】是否存在点M,使得△AQM为直角三角形?若存在,求出点M的坐标,若不存在,
![]() 说明理由.
说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,利用一面墙(墙的长度不超过45m),用80m长的篱笆围一个矩形场地.
(1)怎样围才能使矩形场地的面积为750m2?
(2)能否使所围矩形场地的面积为810m2 ,为什么?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com