【题目】如图，木杆AB斜靠在墙壁上，∠OAB=30°，AB=4米．当木杆的上端A沿墙壁NO下滑时，木杆的底端B也随之沿着地面上的射线OM方向滑动．设木杆的顶端A匀速下滑到点O停止，则木杆的中点P到射线OM的距离y（米）与下滑的时间x（秒）之间的函数图象大致是（ ）
A.
B.
C.
D.
【答案】B
【解析】解：如图，过点P作PQ⊥OB于点Q，
∴PQ∥OA，
∵P为AB中点，
∴PQ为△AOB的中位线，即PQ= 
OA，
∵∠OAB=30°，AB=4，
∴OA=ABcos∠OAB=4× 
=2 
，
则OP= ，
当点A匀速向下滑动时，OA的长度随时间x的变化满足一次函数关系，
由于PQ= OA，
∴PQ的长度与下滑时间满足一次函数关系，且PQ的最大值为 ，符合题意得只有B选项，
故选：B．
【考点精析】本题主要考查了一次函数的图象和性质的相关知识点，需要掌握一次函数是直线，图像经过仨象限；正比例函数更简单,经过原点一直线；两个系数k与b,作用之大莫小看，k是斜率定夹角,b与Y轴来相见,k为正来右上斜,x增减y增减；k为负来左下展,变化规律正相反；k的绝对值越大,线离横轴就越远才能正确解答此题．
科目：初中数学 来源： 题型：
【题目】如图①，将笔记本活页一角折过去，使角的顶点A落在A′处，BC为折痕．
(1)图①中，若∠1=30
，求∠A′BD的艘数；
(2)如果将图①的另一角∠A′BD斜折过去，使BD边与BA′重合，折痕为BE，点D的对应点为D′，如图②所示．∠1=30
，求∠2以及∠CBE的度数；
(3)如果将图①的另一角斜折过去，使BD边落在∠l内部，折痕为BE，点D的对应点为D′，如图③所示，若∠1=40
，设∠A′BD′=α，∠EBD=β，请直接回答：
①α的取值范围和β的取值范围：
②α与β之间的数量关系．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，顺次连接四边形ABCD各边中点得四边形EFGH，要使四边形EFGH为矩形，应添加的条件是（ ）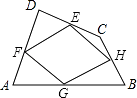 
A.AB∥DC
B.AC=BD
C.AC⊥BD
D.AB=DC
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平脉直角坐标系中，已知点A（2﹣a，2a+3）在第四象限．
（1）若点A到x轴的距离与到y轴的距离相等，求a的值；
（2）若点A到x轴的距离小于到y轴的距离，求a的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】2017年6月5日是第46个“世界环境日”，为提高学生的环保意识，某校组织该校2000名学生参加了“环保知识”竞赛，为了解“环保知识”的笔试情况，学校随机抽取了部分参赛同学的成绩，整理并绘制成如图所示的不完整的图表．
分数段 | 频数 | 频率 |
60≤x＜70 | 30 | 0.1 |
70≤x＜80 | 90 | n |
80≤x＜90 | m | 0.4 |
90≤x＜100 | 60 | 0.2 |
请你根据表中提供的信息，解答下列问题：
（1）此次调查的样本容量为；
（2）在表中：m= ， n=；
（3）补全频数分布直方图；
（4）如果比赛成绩80分以上（含80分）为优秀，那么请你估计该校学生笔试成绩的优秀人数大约是名．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图1，在线段AB中，已知AD＝2，DF＝6，FB＝1，有人想把线段
分成三段： 
、EG、GC，使得
：EG：GC＝2：6：1，他把线段AB移到
的位置（即把A移到
，把B移到
），连接
，分别过
、
作
∥
∥
．
（1）若
＝4.5，则EG＝ ， 
＝ ；
（2）上述方法启发我们可以解决下列问题：如图2，已知△ABC和线段a，请用直尺与圆规作
，满足：
①
∽△ABC；
②
的周长等于线段a的长度．（保留作图痕迹，并写出作图步骤）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】下列哪些线段能组成三角形（ ）
①3cm、3cm、5cm ②3cm、3cm、3cm ③2cm、2cm、4cm ④3cm、5cm、9cm
A.①②B.③④C.①②③D.①②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
