
【题目】按下列程序进行运算(如图)
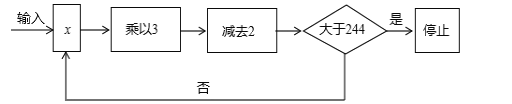
规定:程序运行到“判断结果是否大于244”为一次运算,若运算进行了5次才停止,则x的取值范围是 .
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案科目:初中数学 来源: 题型:
【题目】计算下列各题(直接写出答案)
(1)2+(﹣2)= ;
(2)1﹣3= ;
(3)(﹣1)×(﹣3)= ;
(4)12÷(﹣3)= ;
(5)﹣32×![]() = ;
= ;
(6)(﹣4)2018×(﹣0.25)2019= ;
查看答案和解析>>
科目:初中数学 来源: 题型:
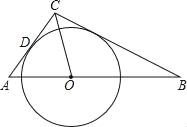
【题目】如图,在△ABC中,∠C=90°,∠ACB的平分线交AB于点O,以O为圆心的⊙O与AC相切于点D.
(1)求证:⊙O与BC相切;
(2)当AC=3,BC=6时,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义一种运算:![]() ,其中k是正整数,且k ≥2,[x]表示非负实数x的整数部分,例如[2.6]=2,[0.8]=0.若
,其中k是正整数,且k ≥2,[x]表示非负实数x的整数部分,例如[2.6]=2,[0.8]=0.若![]() ,则
,则![]() 的值为( )
的值为( )
A.2015B.4C.2014D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】当前,交通拥堵是城市管理的一大难题.我市城东高架桥的开通为分流过境车辆、缓解市内交通压力 起到了关键作用,但为了保证安全,高架桥上最高限速 80 千米/小时.在一般条件下,高架桥上的车流 速度 v(单位:千米/小时)是车流密度 x(单位:辆/千米)的函数,当桥上的车流密度达到 180 辆/千 米时,造成堵塞,此时车流速度为 0;当 0≤x≤20 时,桥上畅通无阻,车流速度都为 80 千米/小时, 研究表明:当 20≤x≤180 时,车流速度 v 是车流密度 x 的一次函数.
(1)当 0≤x≤20 和 20≤x≤180 时,分别写出函数 v 关于 x 的函数关系式;
(2)当车流密度 x 为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时)w=x·v可以达到最大,并求出最大值;
(3)某天早高峰(7:30—9:30)经交警部门控制管理,桥上的车流速度始终保持 40 千米/小时,问这天 早高峰期间高架桥分流了多少辆车?
查看答案和解析>>
科目:初中数学 来源: 题型:
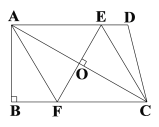
【题目】已知:如图,在四边形ABCD中,AD∥BC,∠B=90°,对角线AC的垂直平分线与边AD、BC分别相交于点E、F.
(1)求证:四边形AFCE是菱形;
(2)若AB=6,BC=8,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,O为直线AB上一点,过点O作射线OC,∠AOC=30°,将一直角三角板(∠M=30°)的直角项点放在点O处,一边ON在射线OA上,另一边OM与OC都在直线AB的上方.
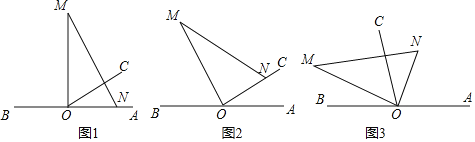
(1)将图1中的三角板绕点O以每秒5°的速度沿逆时针方向旋转一周.如图2,经过t秒后,ON落在OC边上,则t= 秒(直接写结果).
(2)在(1)的条件下,若三角板继续转动,同时射线OC也绕O点以每秒10°的速度沿逆时针方向旋转一周,当OC转动9秒时,求∠MOC的度数.
(3)在(2)的条件下,它们继续运动多少秒时,∠MOC=35°?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
小炎遇到这样一个问题:如图1,点E、F分别在正方形ABCD的边BC,CD上,∠EAF=45°,连结EF,则EF=BE+DF,试说明理由.

小炎是这样思考的:要想解决这个问题,首先应想办法将这些分散的线段相对集中.她先后尝试了翻折、旋转、平移的方法,最后发现线段AB,AD是共点并且相等的,于是找到解决问题的方法.她的方法是将△ABE绕着点A逆时针旋转90°得到△ADG,再利用全等的知识解决了这个问题(如图2).
参考小炎同学思考问题的方法,解决下列问题:
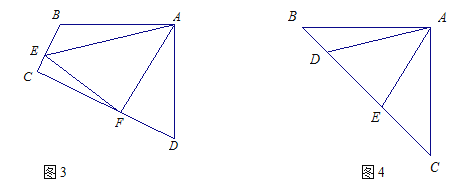
(1)如图3,四边形ABCD中,AB=AD,∠BAD=90°点E,F分别在边BC,CD上,∠EAF=45°.若∠B,∠D都不是直角,则当∠B与∠D满足_ 关系时,仍有EF=BE+DF;
(2)如图4,在△ABC中,∠BAC=90°,AB=AC,点D、E均在边BC上,且∠DAE=45°,若BD=1, EC=2,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校将举行“亲近大自然”户外活动.现随机抽取了部分学生进行了“你最想去的景点”的问卷调查,要求学生只能从A,B,C,D四个景点中选择一个.根据调查结果,绘制了如下两幅不完整的统计图.
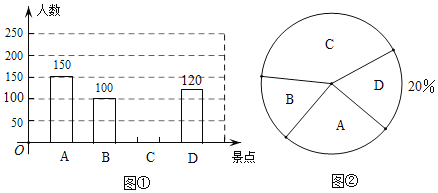
(1)本次调查共调查了______名学生;
(2)补全图①中的条形统计图,图②中最想去景点C的圆心角的度数为______°.
(3)已知该校共有2400名学生,估计最想去景点C的学生人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com