
【题目】定义一种运算:![]() ,其中k是正整数,且k ≥2,[x]表示非负实数x的整数部分,例如[2.6]=2,[0.8]=0.若
,其中k是正整数,且k ≥2,[x]表示非负实数x的整数部分,例如[2.6]=2,[0.8]=0.若![]() ,则
,则![]() 的值为( )
的值为( )
A.2015B.4C.2014D.5
【答案】B
【解析】
首先定义的新运算方法,可得a2=a1+1-5([![]() ]-[
]-[![]() ])=1+1=2,a3=a2+1-5([
])=1+1=2,a3=a2+1-5([![]() ]-[
]-[![]() ])=2+1=3,同理,可得a4=4,a5=5,a6=1,a7=2,…,所以这列数是1、2、3、4、5、1、2、3、4、5、…,每5个数是一个循环;然后用2014除以4,根据余数的情况判断出a2014的值为多少即可.
])=2+1=3,同理,可得a4=4,a5=5,a6=1,a7=2,…,所以这列数是1、2、3、4、5、1、2、3、4、5、…,每5个数是一个循环;然后用2014除以4,根据余数的情况判断出a2014的值为多少即可.
∵a1=1,
∴a2=a1+1-5([![]() ]-[
]-[![]() ])=1+1=2,
])=1+1=2,
a3=a2+1-5([![]() ]-[
]-[![]() ])=2+1=3,
])=2+1=3,
同理,可得a4=4,a5=5,a6=1,a7=2,…,
所以这列数是1、2、3、4、5、1、2、3、4、5、…,每5个数是一个循环;
∵2014÷5=402…4,
∴a2014=4.
故选B.


科目:初中数学 来源: 题型:
【题目】有4张正面分别标有数字![]() 的不透明卡片,它们除数字不同外其余全部相同,现将它们背面朝上,洗匀后从中任取一张,将卡片上的数字记为
的不透明卡片,它们除数字不同外其余全部相同,现将它们背面朝上,洗匀后从中任取一张,将卡片上的数字记为![]() ,另有一个被均匀分成4份的转盘,上面分别标有数字
,另有一个被均匀分成4份的转盘,上面分别标有数字![]() ,转动转盘,指针所指的数字记为
,转动转盘,指针所指的数字记为![]() (若指针指在分割线上则重新转一次),则点
(若指针指在分割线上则重新转一次),则点![]() 落在抛物线
落在抛物线![]() 与
与![]() 轴所围成的区域内(不含边界)的概率是__________.
轴所围成的区域内(不含边界)的概率是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD对角线交于点O,BE∥AC,AE∥BD,EO与AB交于点F.
(1)试判断四边形AEBO的形状,并说明你的理由;
(2)求证:EO=DC.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,如果 x 与 y 都是整数,就称点(x,y)为整点.下列命题中错误的是( )
A. 存在这样的直线,既不与坐标轴平行,又不经过任何整点
B. 若 k 与 b 都是无理数,则直线 y=kx+b 不经过任何整点
C. 若直线 y=kx+b 经过无数多个整点,则 k 与 b 都是有理数
D. 存在恰好经过一个整点的直线
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小高从家门口骑车去离家4千米的单位上班,先花3分钟走平路1千米,再走上坡路以0.2千米/分钟的速度走了5分钟,最后走下坡路花了4分钟到达工作单位,若设他从家开始去单位的时间为t(分钟),离家的路程为y(千米),则y与t(8<t≤12)的函数关系为( )
A. y=0.5t(8<t≤12) B. y=0.5t+2(8<t≤12)
C. y=0.5t+8(8<t≤12) D. y="0." 5t-2(8<t≤12)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在长方形ABCD中,把△BCD沿对角线BD折叠得到△BED,线段BE与AD相交于点P,若AB=2,BC=4.
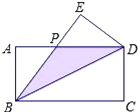
(1)求BD长度;(2)求点P到BD的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程(组)及不等式(组)解应用题:
水是生命之源.为了鼓励市民节约用水,江夏区水务部门实行居民用水阶梯式计量水价政策;若居民每户每月用水量不超过10立方米,每立方米按现行居民生活用水水价收费(现行居民生活用水水价=基本水价+污水处理费);若每户每月用水量超过10立方米,则超过部分每立方米在基本水价基础上加价100%,但每立方米污水处理费不变.
下面表格是某居民小区4月份甲、乙两户居民生活用水量及缴纳生活用水水费的情况统计:
4月份居民用水情况统计表
(注:污水处理的立方数=实际生活用水的立方数)
用水量(立方米) | 缴纳生活用水费用(元) | |
甲用户 | 8 | 27.6 |
乙用户 | 12 | 46.3 |
(1)求每立方米的基本水价和每立方米的污水处理费各是多少?
(2)设这个小区某居民用户5月份用水![]() 立方米,需要缴纳的生活用水水费为
立方米,需要缴纳的生活用水水费为![]() 元.若他5月份生活用水水费计划不超过64元,该用户5月份最多可用水多少立方米?
元.若他5月份生活用水水费计划不超过64元,该用户5月份最多可用水多少立方米?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com