
 ”表示数据输入、输出框;用“
”表示数据输入、输出框;用“ ”表示数据处理和运算框;用“
”表示数据处理和运算框;用“ ”表示数据判断框(根据条件决定执行两条路径中的某一条)
”表示数据判断框(根据条件决定执行两条路径中的某一条)
 ”内,应填×5; 第二个“
”内,应填×5; 第二个“ ”内,应填-3;
”内,应填-3;分析 (1)①把x=-2代入图1中的程序中计算确定出输出数y即可;
②根据输出的代数式确定出程序中应添的运算即可;
(2)①把x=-1代入图3中的程序中计算确定出输出y即可;
②把y=17代入图4中的程序中计算即可确定出输入x的值;
(3)根据题意确定出所求计算框图即可.
解答 解:(1)①把x=-2代入得:y=(-2)×2-5=-4-5=-9;
②根据题意得:第一个“ ”内,应填×5;第二个“
”内,应填×5;第二个“ ”内,应填-3;
”内,应填-3;
(2)①把x=-1代入得:(-1)×2-3=-2-3=-5,
把x=-5代入得:(-5)×2-3=-10-3=-13,
把x=-13代入得:(-13)×2-3=-26-3=-29,
则y=-29;
②若x>0,把y=17代入得:x=17+5=22;
若x<0,把y=17代入得:x=-$\sqrt{17-1}$=-4,
则x=22或-4;
(3)如图所示: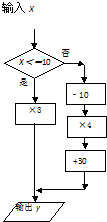
故答案为:(1)①-9;②×;-3;(2)①-29;②22或-4.
点评 此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 1,2 | B. | 0,2 | C. | 2,1 | D. | 1,1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com