
分析 (1)利用乘法公式展开,然后合并同类项即可;
(2)先把括号内通分后进行同分母的减法运算,再把分子分母因式分解和除法运算化为乘法运算,然后约分即可.
解答 解:(1)原式=a2-2ab+b2+2a2-ab-4ab+2b2
=3a2-7ab+3b2;
(2)原式=$\frac{x-3}{{3x({x-2})}}÷\frac{{({x+2})({x-2})-5}}{x-2}$、
=$\frac{x-3}{{3x({x-2})}}÷\frac{{{x^2}-9}}{x-2}$
=$\frac{x-3}{{3x({x-2})}}•\frac{x-2}{{({x+3})({x-3})}}$
=$\frac{1}{{3x({x+3})}}$
=$\frac{1}{{3{x^2}+9x}}$.
点评 本题考查了分式的混合运算:分式的混合运算,要注意运算顺序,式与数有相同的混合运算顺序;先乘方,再乘除,然后加减,有括号的先算括号里面的.最后结果分子、分母要进行约分,注意运算的结果要化成最简分式或整式.也考查了整式的混合运算.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | -1 | C. | 一2 | D. | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
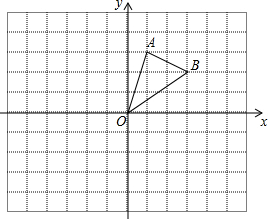 在边长为1的小正方形网格中,△AOB的顶点均在格点上.
在边长为1的小正方形网格中,△AOB的顶点均在格点上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 ”表示数据输入、输出框;用“
”表示数据输入、输出框;用“ ”表示数据处理和运算框;用“
”表示数据处理和运算框;用“ ”表示数据判断框(根据条件决定执行两条路径中的某一条)
”表示数据判断框(根据条件决定执行两条路径中的某一条)
 ”内,应填×5; 第二个“
”内,应填×5; 第二个“ ”内,应填-3;
”内,应填-3;查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,平面直角坐标系中,点P的坐标是(3,4),直线l经过点P且平行于y轴,点Q从点A(3,10)出发,以每秒1个单位长的速度沿AP方向匀速运动.回答下列问题:
如图,平面直角坐标系中,点P的坐标是(3,4),直线l经过点P且平行于y轴,点Q从点A(3,10)出发,以每秒1个单位长的速度沿AP方向匀速运动.回答下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com