
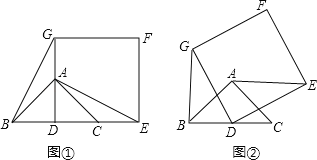
【题目】如图①,已知△ABC是等腰三角形,∠BAC=90°,点D是BC的中点,作正方形DEFG,使点A、C分别在DG和DE上,连接AE、BG.
(1)试猜想线段BG和AE的关系为;
(2)如图②,将正方形DEFG绕点D按逆时针方向旋转α(0°<α≤90°),判断(1)中的结论是否仍然成立,证明你的结论.
【答案】(1)BG=AE.AE⊥BG,理由见解析;(2)成立,理由见解析.
【解析】
(1)由等腰直角三角形的性质及正方形的性质就可以得出△ADE≌△BDG就可以得出结论;
(2)如图2,连接AD,由等腰直角三角形的性质及正方形的性质就可以得出△ADE≌△BDG就可以得出结论;
(1)结论:BG=AE,BG⊥AE.
理由:如图1,延长EA交BG于K.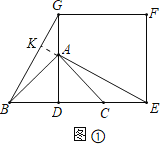
∵△ABC是等腰直角三角形,∠BAC=90°,点D是BC的中点,
∴AD⊥BC,BD=CD,
∴∠ADB=∠ADC=90°.
∵四边形DEFG是正方形,
∴DE=DG.
在△BDG和△ADE中,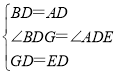 ,
,
∴△ADE≌△BDG(SAS),
∴BG=AE,∠BGD=∠AED,
∵∠GAK=∠DAE,
∴∠AKG=∠ADE=90°,
∴EA⊥BG.
(2)①成立BG=AE.
理由:如图2,连接AD,延长EA交BG于K,交DG于O.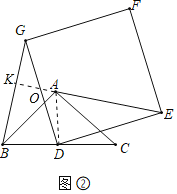
∵在Rt△BAC中,D为斜边BC中点,
∴AD=BD,AD⊥BC,
∴∠ADG+∠GDB=90°.
∵四边形EFGD为正方形,
∴DE=DG,且∠GDE=90°,
∴∠ADG+∠ADE=90°,
∴∠BDG=∠ADE.
在△BDG和△ADE中,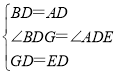 ,
,
∴△BDG≌△ADE(SAS),
∴BG=AE,∠BGD=∠AED,
∵∠GOK=∠DOE,
∴∠OKG=∠ODE=90°,
∴EA⊥BG.


科目:初中数学 来源: 题型:
【题目】如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )

A. CB=CD B. ∠BAC=∠DAC C. ∠BCA=∠DCA D. ∠B=∠D=90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《如果想毁掉一个孩子,就给他一部手机!》这是2017年微信圈一篇热传的文章.国际上,法国教育部宣布从 2018 年9月新学期起小学和初中禁止学生使用手机.为了解学生手机使用情况,某学校开展了“手机伴我健康行”主题活动,他们随机抽取部分学生进行“使用手机目的”和“每周使用手机的时间”的问卷调查,并绘制成如图①,②的 统计图,已知“查资料”的人数是 40人.请你根据以上信息解答下列问题:
(1)在扇形统计图中,“玩游戏”对应的百分比为______,圆心角度数是______度;
(2)补全条形统计图;
(3)该校共有学生2100人,估计每周使用手机时间在2 小时以上(不含2小时)的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
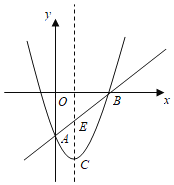
【题目】如图,在平面直角坐标系![]() 中,已知抛物线
中,已知抛物线![]() 与直线
与直线![]() 都经过
都经过![]() 、
、![]() 两点,该抛物线的顶点为C.
两点,该抛物线的顶点为C.
(1)求此抛物线和直线![]() 的解析式;
的解析式;
(2)设直线![]() 与该抛物线的对称轴交于点E,在射线
与该抛物线的对称轴交于点E,在射线![]() 上是否存在一点M,过M作x轴的垂线交抛物线于点N,使点M、N、C、E是平行四边形的四个顶点?若存在,求点M的坐标;若不存在,请说明理由;
上是否存在一点M,过M作x轴的垂线交抛物线于点N,使点M、N、C、E是平行四边形的四个顶点?若存在,求点M的坐标;若不存在,请说明理由;
(3)设点P是直线![]() 下方抛物线上的一动点,当
下方抛物线上的一动点,当![]() 面积最大时,求点P的坐标,并求
面积最大时,求点P的坐标,并求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,E,F分别为AD,BC边上的一点,增加下列条件,不能得出BE∥DF的是( )
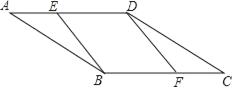
A. AE=CF B. BE=DF C. ∠EBF=∠FDE D. ∠BED=∠BFD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,△ABC的位置如图所示(每个小方格都是边长为1个单位长度的正方形).

(1)将△ABC沿![]() 轴方向向左平移6个单位,画出平移后得到的△A1B1C1;
轴方向向左平移6个单位,画出平移后得到的△A1B1C1;
(2)将△ABC绕着点O顺时针旋转90°,画出旋转后得到的△AB2C2,并直接写出点B2 、C2的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】边长为6的等边△ABC中,点D、E分别在AC、BC边上,DE∥AB,EC=2![]() .
.
(1)如图1,将△DEC沿射线EC方向平移,得到△D′E′C′,边D′E′与AC的交点为M,边C′D′与∠ACC′的角平分线交于点N,当CC′多大时,四边形MCND′为菱形?并说明理由.
(2)如图2,将△DEC绕点C旋转∠α(0°<α<360°),得到△D′E′C,连接AD′、BE′.边D′E′的中点为P.
①在旋转过程中,AD′和BE′有怎样的数量关系?并说明理由;
②连接AP,当AP最大时,求AD′的值.(结果保留根号)
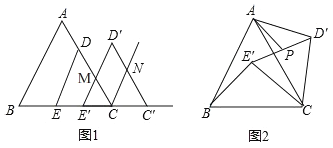
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 经过点
经过点![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
![]() 求这条抛物线的解析式;
求这条抛物线的解析式;
![]() 如图1,点P是第三象限内抛物线上的一个动点,当四边形
如图1,点P是第三象限内抛物线上的一个动点,当四边形![]() 的面积最大时,求点
的面积最大时,求点![]() 的坐标;
的坐标;
![]() 如图2,线段
如图2,线段![]() 的垂直平分线交
的垂直平分线交![]() 轴于点
轴于点![]() ,垂足为
,垂足为![]() 为抛物线的顶点,在直线
为抛物线的顶点,在直线![]() 上是否存在一点
上是否存在一点![]() ,使
,使![]() 的周长最小?若存在,求出点
的周长最小?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为弘扬传统文化,某校开展了“传承经典文化,阅读经典名著”活动.为了解七、八年级学生(七、八年级各有600名学生)的阅读效果,该校举行了经典文化知识竞赛.现从两个年级各随机抽取20名学生的竞赛成绩(百分制)进行分析,过程如下:
收集数据:
七年级:79,85,73,80,75,76,87,70,75,94,75,79,81,71,75,80,86,59,83,77.
八年级:92,74,87,82,72,81,94,83,77,83,80,81,71,81,72,77,82,80,70,41.
整理数据:
|
|
|
|
|
| |
七年级 | 0 | 1 | 0 | a | 7 | 1 |
八年级 | 1 | 0 | 0 | 7 | b | 2 |
分析数据:
平均数 | 众数 | 中位数 | |
七年级 | 78 | 75 |
|
八年级 | 78 |
| 80.5 |
应用数据:
(1)由上表填空:a= ,b= ,c= ,d= .
(2)估计该校七、八两个年级学生在本次竞赛中成绩在90分以上的共有多少人?
(3)你认为哪个年级的学生对经典文化知识掌握的总体水平较好,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com