
【题目】如图,平面直角坐标系中有点B(﹣1,0)和y轴上一动点A(0,a),其中a>0,以A点为直角顶点在第二象限内作等腰直角△ABC,设点C的坐标为(c,d).
(1)当a=2时,则C点的坐标为( , );
(2)动点A在运动的过程中,试判断c+d的值是否发生变化?若不变,请求出其值;若发生变化,请说明理由.
(3)当a=2时,在坐标平面内是否存在一点P(不与点C重合),使△PAB与△ABC全等?若存在,直接写出P点坐标;若不存在,请说明理由.
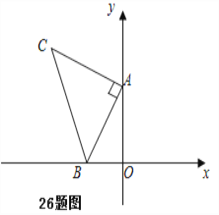
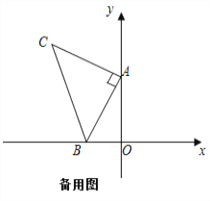
【答案】(1)C(-2,3);(2)c+d的值不变,c+d=1(3)P点坐标(-3,1)、(2,1)、(1,-1).
【解析】试题(1)先过点C作CE⊥y轴于E,证△AEC≌△BOA,推出CE=OA=2,AE=BO=1,即可得出点C的坐标;(2)、先过点C作CE⊥y轴于E,证△AEC≌△BOA,推出CE=OA=a,AE=BO=1,可得OE=a=1,即可得出点C的坐标为(-a,a+1),据此可得c+d的值不变;(3)、分为三种情况讨论,分别画出符合条件的图形,构造直角三角形,证出三角形全等,根据全等三角形对应边相等即可得出答案.
试题解析:(1)、C(-2,3);
(2)、 动点A在运动的过程中c+d的值不变.
过点C作CE⊥y轴于E,则∠CEA=∠AOB, ∵△ABC是等腰直角三角形,
∴AC=BA,∠BAC=90°,∴∠ACE+∠CAE=90°=∠BAO+∠CAE,∴∠ACE=∠BAO,
∴△ACE≌△BAO, ∵B(-1,0),A(0,a),∴BO=AE=1,AO=CE=a,
∴OE=a+1,∴C(-a,1+a), 又∵点C的坐标为(c,d),
∴c+d=-a+1+a=1,即c+d的值不变;
(3)、P点坐标(-3,1)、(2,1)、(1,-1).


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,直线y=-x+m分别交于x轴、y轴于A,B两点,已知点C(2,0).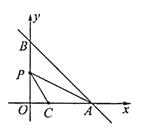
(1)当直线AB经过点C时,点O到直线AB的距离是;
(2)设点P为线段OB的中点,连结PA,PC,若∠CPA=∠ABO,则m的值是.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
∵![]() ,
,![]() ,
,![]() ,……
,……![]() ,
,
∴![]()
=![]()
=![]() =
=![]() .
.
解答下列问题:
(1)在和式![]() 中,第6项为______,第n项是__________.
中,第6项为______,第n项是__________.
(2)上述求和的想法是通过逆用________法则,将和式中的各分数转化为两个数之差,使得除首末两项外的中间各项可以_______,从而达到求和的目的.
(3)受此启发,请你解下面的方程:
![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
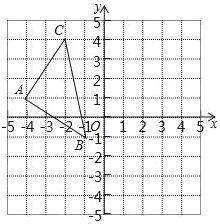
【题目】已知,△ABC在平面直角坐标系中的位置如图所示.
(1)把△ABC向下平移2个单位长度得到△A1B1C1,请画出△A1B1C1;
(2)请画出△A1B1C1关于y轴对称的△A2B2C2,并写出A2的坐标;
(3)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B两地的距离是80千米,一辆公共汽车从A地驶出3小时后,一辆小汽车也从A地出发,它的速度是公共汽车的3倍,已知小汽车比公共汽车迟20分钟到达B地,求两车的速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】化简.
(1)( x- y)( x+ y) ( x2+ y2) ( x4+ y4)·…·(x16+ y16);
(2)(22+1)(24+1)(28+1)(216+1).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为响应珠海环保城市建设,我市某污水处理公司不断改进污水处理设备,新设备每小时处理污水量是原系统的1.5倍,原来处理1200m3污水所用的时间比现在多用10小时.
(1)原来每小时处理污水量是多少m2?
(2)若用新设备处理污水960m3,需要多长时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,CD为AB边上的高
(1) 如图1,求证:∠BAC=2∠BCD
(2) 如图2,∠ACD的平分线CE交AB于E,过E作EF⊥BC于F,EF与CD交于点G.若ED=m,BD=n,请用含有m、n的代数式表示△EGC的面积
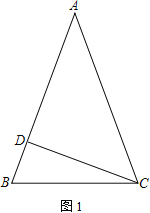
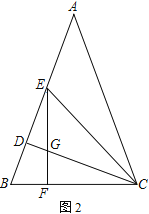
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com