
【题目】如图,矩形![]() ,点
,点![]() 、
、![]() 分别在
分别在![]() 轴、
轴、![]() 轴上, 点
轴上, 点![]() 坐标为
坐标为![]() , 连接
, 连接![]() ,将矩形
,将矩形![]() 沿
沿![]() 折叠,点
折叠,点![]() 的对应点为点
的对应点为点![]() ,则点
,则点![]() 的坐标为_____(用含
的坐标为_____(用含![]() 的式子表示).
的式子表示).
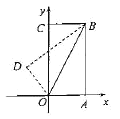
【答案】![]()
【解析】
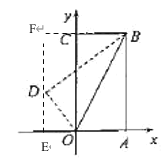
过点D做DE⊥x轴,垂足为E,交BC延长线于点F.证明△OED∽△DFB,相似比为1:2,设DE=m,表示各线段关系,求出m,进而求出点![]() 的坐标.
的坐标.
解:如图,过点D做DE⊥x轴,垂足为E,交BC延长线于点F.
∵矩形![]() 中,点
中,点![]() 坐标为
坐标为![]() ,
,
∴OA=k,AB=2k.
∵矩形![]() 沿
沿![]() 折叠,
折叠,
∴△OBD≌△OBA,
∴OD= OA=k,BD=BA=2k,∠ODB=∠OAB=90°,
∴∠FDB+∠EDO=90°.
∵∠EOD+∠EDO=90°,
∴∠EOD=∠FDB.
∵∠F=∠DEO=90°,
∴△OED∽△DFB,
∴![]() .
.
设DE=m,则BF=2m,OE=2m-k,
∴2k-m=2(2m-k)
∴![]() ,
,
∴![]()
∴点D坐标为:![]() .
.
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】某市为解决部分市民冬季集中取暖问题需铺设一条长3000米的管道,为尽量减少施工对交通造成的影响,实施施工时“…”,设实际每天铺设管道x米,则可得方程 ![]() ,根据此情景,题中用“…”表示的缺失的条件应补为( )
,根据此情景,题中用“…”表示的缺失的条件应补为( )
A.每天比原计划多铺设10米,结果延期15天才完成
B.每天比原计划少铺设10米,结果延期15天才完成
C.每天比原计划多铺设10米,结果提前15天才完成
D.每天比原计划少铺设10米,结果提前15天才完成
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,三个半圆依次相外切,它们的圆心都在x轴的正半轴上并与直线y=![]() x相切,设半圆C1、半圆C2、半圆C3的半径分别是r1、r2、r3 , 则当r1=1时,r3= .
x相切,设半圆C1、半圆C2、半圆C3的半径分别是r1、r2、r3 , 则当r1=1时,r3= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校开展的“书香校园”活动受到同学们的广泛关注,为了解全校学生课外阅读的情况,随机调查了部分学生在一周内借阅图书的次数,并制成如图不完整的统计图表.
学生借阅图书的次数统计表:
借阅图书的次数 |
|
|
|
|
|
人数 |
|
|
|
|
|

请你根据统计图表中的信息,解答下列问题:
(1)![]() ,
,![]() ;
;
(2)该调查统计数据的中位数是 ,众数是 ;
(3)若该校共有![]() 名学生,根据调查结果,估计该校学生在一周内借阅图书
名学生,根据调查结果,估计该校学生在一周内借阅图书![]() 次及以上的人数.
次及以上的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】入冬以来,我省的雾霾天气频发,空气质量较差,容易引起多种上呼吸道疾病.某电器商场代理销售![]() ,
,![]() 两种型号的家用空气净化器,已知一台
两种型号的家用空气净化器,已知一台![]() 型空气净化器的进价比一台
型空气净化器的进价比一台![]() 型空气净化器的进价高200元;2台
型空气净化器的进价高200元;2台![]() 型空气净化器的进价与3台
型空气净化器的进价与3台![]() 型空气净化器的进价相同.
型空气净化器的进价相同.
(1)求![]() ,
,![]() 两种型号的家用空气净化器的进价分别是多少元.
两种型号的家用空气净化器的进价分别是多少元.
(2)若商场购进这两种型号的家用空气净化器共50台,其中![]() 型家用空气净化器的数量不超过
型家用空气净化器的数量不超过![]() 型家用空气净化器的数量,且不少于16台,设购进
型家用空气净化器的数量,且不少于16台,设购进![]() 型家用空气净化器
型家用空气净化器![]() 台.
台.
①求![]() 的取值范围;
的取值范围;
②已知![]() 型家用空气净化器的售价为每台800元,销售成本为每台
型家用空气净化器的售价为每台800元,销售成本为每台![]() 元;
元;![]() 型家用空气净化器的售价为每台550元,销售成本为每台
型家用空气净化器的售价为每台550元,销售成本为每台![]() 元.若
元.若![]() ,求售完这批家用空气净化器的最大利润
,求售完这批家用空气净化器的最大利润![]() (元)与
(元)与![]() (元)的函数关系式.(每台销售利润=售价-进价-销售成本)
(元)的函数关系式.(每台销售利润=售价-进价-销售成本)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:用2辆A型车和1辆B型车装满货物一次可运货10t;用1辆A型车和2辆B型车装满货物一次可运货11t.某物流公司现有35t货物,计划同时租用A型车a辆,B型车b辆,一次运完,且恰好每辆车都装满货物.根据以上信息,解答下列问题:
(1)1辆A型车和1辆B型车都装满货物一次可分别运货多少吨?
(2)请你帮该物流公司设计租车方案;
(3)若A型车每辆需租金100元/次,B型车每辆需租金120元/次.请选出最省钱的租车方案,并求出最少租车费.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】整式运算
(1)(x4)3÷(﹣x2)2+(﹣x2)3x2
(2)(x+3)(x﹣5)+2x(3x﹣1)
(3)(2b﹣a)(2a+b)﹣2(3a﹣2b)2
(4)![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,点P是Rt△ABC斜边AB上一动点(不与A、B重合),分别过A、B向直线CP作垂线,垂足分别为E、F、Q为斜边AB的中点.
(1)如图1,当点P与点Q重合时,AE与BF的位置关系,QE与QF的数量关系.
(2)如图2,当点P在线段AB上不与点Q重合时,试判断QE与QF的数量关系,并给予证明;
(3)如图3,当点P在线段BA(或AB)的延长线上时,此时(2)中的结论是否成立?请画出图形并给予证明.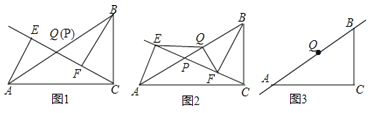
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知直线PQ∥MN,点A、B分别在直线MN、PQ上,射线AM绕点A以5°/秒的速度按顺时针开始旋转,旋转至与AN(或AM)重合后便立即回转,射线BQ绕点B以2°/秒的速度按顺时针开始旋转,旋转至与BP重合后便停止转动,旋转后的射线分别记为AM'和BQ'.
(1)若射线BQ先转动30秒,射线AM才开始转动,在射线AM第一次到达AN之前,射线AM转动几秒后AM'∥BQ';
(2)若射线AM,BQ同时转动t秒,在射线BQ停止转动之前,记射线AM'与BQ'交于点H,若∠AHB=90°,求t的值;
(3)射线AM,BQ同时转动,在射线AM第一次到达AN之前,记射线AM'与BQ'交于点K,过K作KC⊥AK交PQ于点C,如图2,若∠BAN=30°,则在旋转过程中,∠BAK与∠BKC有何数量关系?并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com