
【题目】如图,在![]() ABC中,∠C=90,BD是
ABC中,∠C=90,BD是![]() ABC的一条角一平分线,点O、E、F分别在BD、BC、AC上,且四边形OECF是正方形,
ABC的一条角一平分线,点O、E、F分别在BD、BC、AC上,且四边形OECF是正方形,

(1)求证:点O在∠BAC的平分线上;
(2)若AC=5,BC=12,求OE的长
【答案】(1)证明见解析;(2)2.
【解析】
(1)考察角平分线定理的性质,及直角三角形全等的判断方法,“HL”;(2)利用全等得到线段AM=BE,AM=AF,利用正方形OECF,得到四边都相等,从而利用OE与BE、AF及AB的关系求出OE的长
解:(1)过点O作OM⊥AB于点M
∵正方形OECF
∴OE=EC=CF=OF,OE⊥BC于E,OF⊥AC于F
∵BD平分∠ABC,OM⊥AB于M,OE⊥BC于E
∴OM=OE=OF
∵OM⊥AB于M, OE⊥BC于E
∴∠AMO=90°,∠AFO=90°
∵![]()
∴Rt△AMO≌Rt△AFO
∴∠MA0=∠FAO
∴点O在∠BAC的平分线上
(2)∵Rt△ABC中,∠C=90°,AC=5,BC=12
∴AB=13
∴BE=BM,AM=AF
又BE=BC-CE,AF=AC-CF,而CE=CF=OE
∴BE=12-OE,AF=5-OE
∴BM+AM=AB
即BE+AF=13
12-OE+5-OE=13
解得OE=2



 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】某地为了鼓励居民节约用水,决定实行两级收费制,即每月用水量不超过14吨(含14吨)时,每吨按政府补贴优惠价收费;每月超过14吨时,超过部分每吨按市场调节价收费,小英家1月份用水20吨,交水费29元;2月份用水18吨,交水费24元.
(1)求每吨水的政府补贴优惠价和市场调节价分别是多少?
(2)小英家3月份用水24吨,她家应交水费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠MON=45°,P为∠MON内一点,A为OM上一点,B为ON上一点,当![]() PAB的周长取最小值时,∠APB的度数为( )
PAB的周长取最小值时,∠APB的度数为( )

A.80°B.90°C.110°D.120°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是△ABC的角平分线,DF⊥AB,垂足为F,DE=DG,△ADG和△AED的面积分别为50和38,则△EDF的面积为( )

A. 6B. 12C. 4D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,若∠DAB的角平分线AE交CD于E,连接BE,且BE边平分∠ABC,则以下命题不正确的个数是①BC+AD=AB;②E为CD中点;③∠AEB=90°;④S△ABE=![]() S四边形ABCD;⑤BC=CE.( )
S四边形ABCD;⑤BC=CE.( )

A. 0个 B. 1个 C. 2个 D. 3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①, 已知△ABC中, ∠BAC=90°, AB=AC, AE是过A的一条直线, 且B、C在AE的异侧, BD⊥AE于D, CE⊥AE于E.

(1)求证: BD=DE+CE.
(2)若直线AE绕A点旋转到图②位置时(BD<CE), 其余条件不变, 问BD与DE、CE的数量关系如何? 请给予证明;
(3)若直线AE绕A点旋转到图③位置时(BD>CE), 其余条件不变, 问BD与DE、CE的数量关系如何? 请直接写出结果, 不需证明.
(4)根据以上的讨论,请用简洁的语言表达BD与DE,CE的数量关系。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与x轴,y轴分别交于B,C两点,抛物线
与x轴,y轴分别交于B,C两点,抛物线![]() 过点B,C.
过点B,C.
(1)求b、c的值;
(2)若点D是抛物线在x轴下方图象上的动点,过点D作x轴的垂线,与直线BC相交于点E.当线段DE的长度最大时,求点D的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校计划一次性购买排球和篮球,每个篮球的价格比排球贵30元;购买2个排球和3个篮球共需340元.
(1)求每个排球和篮球的价格:
(2)若该校一次性购买排球和篮球共60个,总费用不超过3800元,且购买排球的个数少于39个.设排球的个数为m,总费用为y元.
①求y关于m的函数关系式,并求m可取的所有值;
②在学校按怎样的方案购买时,费用最低?最低费用为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
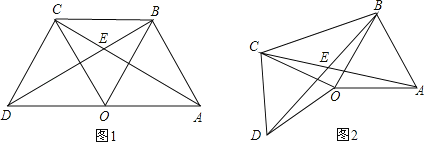
【题目】(1)如图1,点O是线段AD的中点,分别以AO和DO为边在线段AD的同侧作等边三角形OAB和等边三角形OCD,连接AC和BD,相交于点E,连接BC.求∠AEB的大小;
(2)如图2,△OAB固定不动,保持△OCD的形状和大小不变,将△OCD绕点O旋转(△OAB和△OCD不能重叠),求∠AEB的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com