
【题目】某服装厂生产一种围巾和手套,每条围巾的定价为50元,每双手套的定价为20元厂家在开展促销活动期间,向客户提供两种优惠方案:
方案①:买一条围巾送一双手套;
方案②:围巾和手套都按定价的![]() 付款.
付款.
现某客户要到该服装厂购买围巾20条,手套![]() 双(
双(![]() ).
).
(1)若该客户按方案①购买,则需付款______元(用含![]() 的代数式表示);
的代数式表示);
若该客户按方案②购买,则需付款______元(用含![]() 的代数式表示);
的代数式表示);
(2)若![]() ,通过计算说明按哪种方案购买较便宜.
,通过计算说明按哪种方案购买较便宜.
【答案】(1)![]() ;
;![]() ;(2)方案①购买较便宜
;(2)方案①购买较便宜
【解析】
(1)根据买一条围巾送一双手套,现某客户要到该服装厂买围巾20条,可赠送手套20双,则手套付款的有(x-20)双即可得出需付款数;根据围巾和手套都按定价的![]() 付款,每条围巾的定价为50元,每双手套的定价为20元,现某客户要到该服装厂购买围巾20条,手套
付款,每条围巾的定价为50元,每双手套的定价为20元,现某客户要到该服装厂购买围巾20条,手套![]() 双即可得出需付款数;
双即可得出需付款数;
(2)根据(1)中付款方式,将x=30代入求出哪种方案购买较为合算即可.
(1)按方案①购买:50×20+(x20)×20=1000+20x-400=![]() 元;
元;
按方案②购买:(50×20+20x)×0.8=(1000+20x)×0.8=![]() 元;
元;
故答案为:![]() 元;
元;![]() 元
元
(2)把x=30分别代入方案①和方案②得,
方案①:原式![]() (元);
(元);
方案②:原式![]() (元);
(元);
因为![]() ;
;
所以:按方案①购买较便宜.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某地区在一次九年级数学做了检测中,有一道满分8分的解答题,按评分标准,所有考生的得分只有四种:0分,3分,5分,8分.老师为了了解学生的得分情况与题目的难易情况,从全区4500名考生的试卷中随机抽取一部分,通过分析与整理,绘制了如下两幅图不完整的统计图.
请根据以上信息解答下列问题:
(1)填空:a= ,b= ,并把条形统计图补全;
(2)请估计该地区此题得满分(即8分)的学生人数;
(3)已知难度系数的计算公式为L=![]() ,其中L为难度系数,X为样本平均得分,W为试题满分值.一般来说,根据试题的难度系数可将试题分为以下三类:当0<L≤0.4时,此题为难题;当0.4<L≤0.7时,此题为中等难度试题;当0.7<L<1时,此题为容易题.试问此题对于该地区的九年级学生来说属于哪一类?
,其中L为难度系数,X为样本平均得分,W为试题满分值.一般来说,根据试题的难度系数可将试题分为以下三类:当0<L≤0.4时,此题为难题;当0.4<L≤0.7时,此题为中等难度试题;当0.7<L<1时,此题为容易题.试问此题对于该地区的九年级学生来说属于哪一类?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解八年级学生课外阅读情况,随机抽取20名学生平均每周用于课外阅读读的时间(单位:![]() ),过程如下:
),过程如下:
(收集数据)
30 | 60 | 81 | 50 | 40 | 110 | 130 | 146 | 90 | 100 |
60 | 81 | 120 | 140 | 70 | 81 | 10 | 20 | 100 | 81 |
(整理数据)
课外阅读时间 |
|
|
|
|
等级 |
|
|
|
|
人数 | 3 |
| 8 |
|
(分析数据)
平均数 | 中位数 | 众数 |
80 |
|
|
请根据以上提供的信息,解答下列问题:
(1)填空:![]() ______,
______,![]() ______,
______,![]() ______,
______,![]() ______;
______;
(2)如果每周用于课外读的时间不少于![]() 为达标,该校八年级现有学生200人,估计八年级达标的学生有多少人?
为达标,该校八年级现有学生200人,估计八年级达标的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() ,正方形
,正方形![]() 的点
的点![]() 在线段
在线段![]() 上,点
上,点![]() ,
,![]() 在
在![]() 轴正半轴上,点
轴正半轴上,点![]() 在点
在点![]() 的右侧,
的右侧,![]() .将正方形
.将正方形![]() 沿
沿![]() 轴正方向平移,得到正方形
轴正方向平移,得到正方形![]() ,当点
,当点![]() 与点
与点![]() 重合时停止运动.设平移的距离为
重合时停止运动.设平移的距离为![]() ,正方形
,正方形![]() 与
与![]() 重合部分的面积为
重合部分的面积为![]() .
.
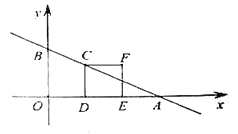
(1)求直线![]() 的解析式;
的解析式;
(2)求点![]() 的坐标;
的坐标;
(3)求![]() 与
与![]() 的解析式,并直接写出自变量
的解析式,并直接写出自变量![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】外卖小哥骑车从商家出发,向东骑了3千米到达小林家,继续骑2.5千米到达小红家,然后向西骑了10千米到达小明家,最后返回商家。
(1)以商家为原点,以向东的方向为正方向,用1个单位长度表示1千米,在数轴上表示出小明家,小林家,小红家的位置。(小林家用点A表示,小红家用点B表示,小明家用点C表示)
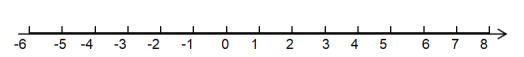
(2)小明家距小林家______千米
(3)若外卖小哥在骑车过程中每千米耗时3分钟,那么外卖小哥在整个过程中共用时多久?(假设外卖小哥一直在匀速行驶,在每户人家上门送外卖的时间忽略不计)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班“数学兴趣小组”对函数y=![]() +x的图象与性质进行了探究,探究过程如下,请补充完整.
+x的图象与性质进行了探究,探究过程如下,请补充完整.
(1)函数y=![]() +x的自变量x的取值范围是 ;
+x的自变量x的取值范围是 ;
(2)下表是y与x的几组对应值.
x | … | ﹣3 | ﹣2 | ﹣1 | 0 | |
|
|
| 2 | 3 | 4 | 5 | … |
y | … | ﹣ | ﹣ | ﹣ | ﹣1 | ﹣ | ﹣ |
|
| 3 |
| m |
| … |
则m= ;
(3)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点,根据描出的点,画出该函数的图象;
(4)该函数的图象关于点( , )成中心对称;
(5)直线y=m与该函数的图象无交点,则m的取值范围为 .
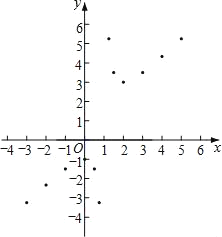
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A是抛物线![]() 上的一个动点,且点A在第一象限内.AE⊥y轴于点E,点B坐标为(0,2),直线AB交
上的一个动点,且点A在第一象限内.AE⊥y轴于点E,点B坐标为(0,2),直线AB交![]() 轴于点C,点D与点C关于y轴对称,直线DE与AB相交于点F,连结BD.设线段AE的长为m,△BED的面积为S.
轴于点C,点D与点C关于y轴对称,直线DE与AB相交于点F,连结BD.设线段AE的长为m,△BED的面积为S.
(1)当![]() 时,求S的值.
时,求S的值.
(2)求S关于![]() 的函数解析式.
的函数解析式.
(3)①若S=![]() 时,求
时,求![]() 的值;
的值;
②当m>2时,设![]() ,猜想k与m的数量关系并证明.
,猜想k与m的数量关系并证明.
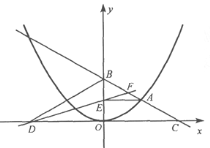
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在下列条件中①∠A∶∠B∶∠C=1∶1∶2,②∠A +∠B=∠C,③∠B =90°-∠A,④∠A=∠B=![]() ∠C,⑤
∠C,⑤![]() 中,能确定△ABC是直角三角形的条件有_________
中,能确定△ABC是直角三角形的条件有_________
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com