Question

1．如图，每个小正方形的边长为1．
（1）求四边形ABCD的面积；
（2）求∠BCD的度数．

Answer 1

分析 （1）根据四边形ABCD的面积=S_矩形AEFH-S_△AEB-S_△BFC-S_△CGD-S_梯形AHGD即可得出结论；
（2）先根据锐角三角函数的定义判断出∠FBC=∠DCG，再根据直角三角形的性质可得出∠BCF+∠DCG=90°，故可得出结论．

解答 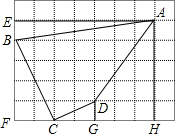解：（1）∵四边形ABCD的面积
=S_矩形AEFH-S_△AEB-S_△BFC-S_△CGD-S_梯形AHGD
=5×7-$\frac{1}{2}$×1×7-$\frac{1}{2}$×2×4-$\frac{1}{2}$×1×2-$\frac{1}{2}$（1+5）×3
=35-$\frac{7}{2}$-4-1-9
=17.5；
（2）∠BCD=90°；理由如下：
∵tan∠FBC=$\frac{2}{4}$=$\frac{1}{2}$，tan∠DCG=$\frac{1}{2}$，
∴∠FBC=∠DCG，
∵∠FBC+∠BCF=∠DCG+∠CDG=90°，
∴∠BCF+∠DCG=90°，
∴∠BCD=90°．

点评 本题考查的是勾股定理、三角函数以及三角形面积的计算，熟知勾股定理及直角三角形的性质是解答此题的关键．