Question

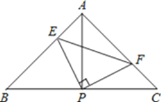
【题目】如图：已知△ABC中，AB=AC，∠BAC=90°，直角∠EPF的顶点P是BC边上的中点，两边PE，PF分别交AB，AC于点E，F，给出以下四个结论：①AE=CF；②EF=AP；③2S四边形AEPF=S△ABC；④当∠EPF在△ABC内绕顶点P旋转时（点E不与A，B重合）有BE+CF=EF；上述结论中始终正确的序号有（ ）个

A.1个B.2个C.3个D.4个

Answer 1

【答案】B

【解析】

根据 “角边角”证明△APE和△CPF全等，根据全等三角形的可得AE=CF，判定①正确，根据等腰直角三角形的斜边等于直角边的 倍表示出EF，可知EF随着点E的变化而变化，判定②错误, 根据全等三角形的面积相等可得△APE的面积等于△CPF的面积相等，然后求出四边形AEPF的面积等于△ABC的面积的一半，判定③正确．根据等腰直角三角形的斜边等于直角边的倍表示出EF，可知EF随着点E的变化而变化，判定④错误．

解：如图，连接EF，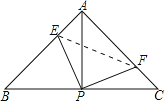
∵AB=AC，∠BAC=90°，点P是BC的中点，

∴AP⊥BC，AP=PC，∠EAP=∠C=45°，

∴∠APF+∠CPF=90°，

∵∠EPF是直角，

∴∠APF+∠APE=90°，

∴∠APE=∠CPF，；

在△APE和△CPF中， ，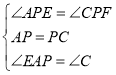

∴△APE≌△CPF（ASA），

∴AE=CF，故①正确；

∵△APE≌△CPF

∴EP=FP

∴△EFP是等腰直角三角形，

∴EF=PF，

而只有F点为AC的中点时，AP=PF，

即点F为AC的中点时有EF=AP，所以②不一定正确．

∵△APE≌△CPF，
∴S△APE=S△CPF，
∴S四边形AEPF=S△APF+S△APE=S△APF+S△CPF=S△APC= S△ABC，

∴2S四边形AEPF=S△ABC

故③正确，

根据等腰直角三角形的性质，EF=PE，

∵EF≤AE+AF，即EF≤AC

∵BE+CF=AC，

∴BE+CF≥EF，故④错误；

综上所述，正确的结论有①③共2个．
故选：B．