
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У���������C1��y=x2+3������ƽ��1����λ��������ƽ��7����λ�õ�������C2 �� C2��ͼ����x�ύ��A��B���㣨��A�ڵ�B����ࣩ��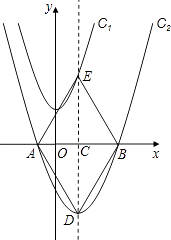
��1����������C2�Ľ���ʽ��
��2����������C2�ĶԳ�����x�ύ�ڵ�C����������C2���ڵ�D����������C1���ڵ�E������AD��DB��BE��EA����֤���ı���ADBE�����Σ����������������
��3������FΪ�Գ���DE������һ�㣬��������C2���Ƿ���������ĵ�G��ʹ��O��B��F��G�ĵ�Ϊ������ı�����ƽ���ı��Σ�������ڣ��������G�����ꣻ��������ڣ���˵�����ɣ�
���𰸡�
��1��
�⣺�߽�������C1��y=x2+3������ƽ��1����λ��������ƽ��7����λ�õ�������C2��
��������C1�Ķ��㣨0��3������ƽ��1����λ��������ƽ��7����λ�õ���1����4����
��������C2�Ķ�������Ϊ��1����4����
��������C2�Ľ���ʽΪy=��x��1��2��4��
��y=x2��2x��3��
��2��
�⣺֤������x2��2x��3=0��
��ã�x1=��1��x2=3��
�ߵ�A�ڵ�B����࣬
��A����1��0����B��3��0����AB=4��
��������C2�ĶԳ���Ϊx=1����������DΪ��1����4����
��CD=4��AC=CB=2��
��x=1����y=x2+3��y=4��
��E��1��4����CE=CD��
���ı���ADBE��ƽ���ı��Σ�
��ED��AB��
���ı���ADBE�����Σ�
S����ADBE=2�� ![]() ��AB��CE=2��
��AB��CE=2�� ![]() ��4��4=16��
��4��4=16��
��3��
�⣺���ڣ���OBΪƽ���ı��εıߺͶԽ������������
�ٵ�OBΪƽ���ı��ε�һ��ʱ����ͼ1��
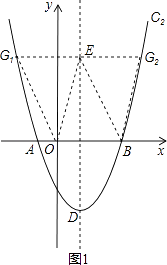
��F��1��y����
��OB=3����G1����2��y����G2��4��y����
�ߵ�G��y=x2��2x��3�ϣ�
�ཫx=��2���룬��y=5����x=4���룬��y=5��
��G1����2��5����G2��4��5����
�ڵ�OBΪƽ���ı��ε�һ�Խ���ʱ����ͼ2��
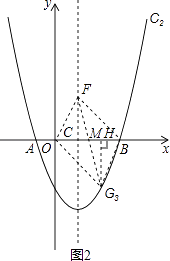
��F��1��y����OB���е�M������G��GH��OB�ڵ�H��
��OB=3��OC=1����OM= ![]() ��CM=
��CM= ![]() ��
��
�ߡ�CFM�ա�HGM��AAS������HM=CM= ![]() ����OH=2��
����OH=2��
��G3��2����y����
�ߵ�G��y=x2��2x��3�ϣ�
�ཫ��2����y�����룬�é�y=��3����y=3��
��G3��2����3����
������������������C2���Ƿ���������ĵ�G��ʹ��O��B��F��G�ĵ�Ϊ������ı�����ƽ���ı��Σ���G������ΪG1����2��5����G2��4��5����G3��2����3����
����������1�����ݶ��κ���ƽ�ƵĹ��ɣ�������Ҽ����ϼ��¼������ó�ƽ�ƺ����ʽ���ɣ���2���������A��B��������꣬�����ö�������ó�AC=CB��CE=CD�������ó��ı���ADBE��ƽ���ı����Լ��ı���ADBE�����Σ������������������ʽ������ɣ���3�����÷�OBΪƽ���ı��εıߺͶԽ�������������ٵ�OBΪƽ���ı��ε�һ��ʱ���ڵ�OBΪƽ���ı��ε�һ�Խ���ʱ�ֱ�ó����ɣ�
�����㾫����������Ŀ����֪���������ö��κ�����ͼ��Ͷ��κ��������ʵ����֪ʶ���Եõ�����Ĵ𰸣���Ҫ���ն��κ���ͼ��ؼ��㣺1�����ڷ���2���Գ��� 3������ 4����x�ύ�� 5����y�ύ�㣻�����ԣ���a>0ʱ���Գ�����ߣ�y��x�������С���Գ����ұߣ�y��x���������a<0ʱ���Գ�����ߣ�y��x��������Գ����ұߣ�y��x�������С��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һԲ��ˮ�ܵĽ���ͼ����֪��O�İ뾶OA=13��ˮ���AB=24����ˮ�����CD�� �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�������P��������y=ax2�ϣ���P�����F��0��n��������ֱ��y=��nʼ�ձ������У���n=���ú�a�Ĵ���ʽ��ʾ����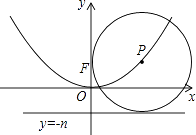
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ���ı���ABCD�У�AB��BC�������²�����ͼ����AΪԲ�ģ�С��AD�ij�Ϊ�뾶�������ֱ�AB��CD��E��F���ٷֱ���E��FΪԲ�ģ����� ![]() EF�ij��뾶�������������ڵ�G��������AG��CD�ڵ�H�������н��ۣ���AGƽ�֡�DAB����CH=
EF�ij��뾶�������������ڵ�G��������AG��CD�ڵ�H�������н��ۣ���AGƽ�֡�DAB����CH= ![]() DH���ۡ�ADH�ǵ��������Σ���S��ADH=
DH���ۡ�ADH�ǵ��������Σ���S��ADH= ![]() S�ı���ABCH ��
S�ı���ABCH ��
������ȷ���У� ��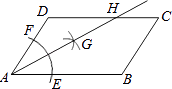
A.�٢ڢ�
B.�٢ۢ�
C.�ڢ�
D.�٢�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڵ�������ABCD�У�DC��AB��E��DC�ӳ����ϵĵ㣬����AE����BC�ڵ�F��
��1����֤����ABF�ס�ECF��
��2�����AD=5cm��AB=8cm��CF=2cm����CE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ֲ�������ŵ�������һ��С·����ͽ�������ų�������������ţ������ͬʱ�����������г��Ӳ�������ǰ�����ŵ������ź���Ϣ0.2Сʱ��Ȼ��ԭ·ԭ�����ٷ��ز��ţ�ͼ�����߷ֱ��ʾ�ס��ҵ����ŵľ���y��km�������ʱ��x��h��֮��ĺ�����ϵͼ����ͼ����Ϣ����������⣺
��1��������ŵľ���y��x֮��ĺ�����ϵʽ��
��2����ס��ҵ�һ������ʱ�����ŵľ��룮
��3����ס��ҵڶ���������ʱ�䣮
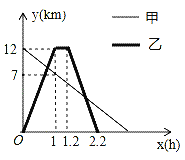
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��AOB�У���AOBΪֱ�ǣ�A����3��a����B��3��b����a+b��12=0�����AOB�����Ϊ_____��
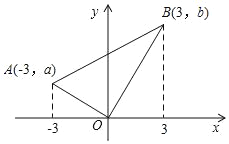
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij������ɲ������ʻ�ľ���s����λ���ף���ʱ��t����λ���룩֮��Ĺ�ϵ�ò����������±���
ʱ��t���룩 | 0 | 0.2 | 0.4 | 0.6 | 0.8 | 1.0 | 1.2 | �� |
��ʻ����s���ף� | 0 | 2.8 | 5.2 | 7.2 | 8.8 | 10 | 10.8 | �� |
�������ֱ仯����һֱ����������ֹͣ��
��1��������Щ�����ڸ���������ϵ�л�����Ӧ�ĵ㣻
��2��ѡ���ʵ��ĺ�����ʾs��t֮��Ĺ�ϵ�������Ӧ�ĺ�������ʽ��
��3����ɲ����������ʻ�˶�����ֹͣ�� �ڵ�t�ֱ�Ϊt1 �� t2��t1��t2��ʱ����Ӧs��ֵ�ֱ�Ϊs1 �� s2 �� ��Ƚ� ![]() ��
�� ![]() �Ĵ�С�������ͱȽϽ����ʵ�����壮
�Ĵ�С�������ͱȽϽ����ʵ�����壮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ֱ�ǡ�ABC�У�б��AB=5��ֱ�DZ�BC��AC֮����һԪ���η���x2����2m��1��x+4��m��1��=0����������m��ֵΪ ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com