
分析 先变形为$\sqrt{{x}^{2}+7}$=$\sqrt{2}x$+1,两边平方得到x2+7=2x2+2$\sqrt{2x}$+1,再变形,利用配方法即可解答此无理方程.
解答 解:∵$\sqrt{{x}^{2}+7}$-$\sqrt{2}x$=1,
∴$\sqrt{{x}^{2}+7}$=$\sqrt{2}x$+1,
∴x2+7=2x2+2$\sqrt{2}$x+1
∴x2+2$\sqrt{2}$x-6=0
∴$(x+\sqrt{2})^{2}$=8,
∴$x+\sqrt{2}=±2\sqrt{2}$,
∴x=$-\sqrt{2}±2\sqrt{2}$,
∴${x}_{1}=-3\sqrt{2}$,${x}_{2}=\sqrt{2}$
点评 此题考查了解无理方程,解无理方程关键是要去掉根号,将其转化为整式方程.解无理方程的基本思想是把无理方程转化为有理方程来解,在变形时要注意根据方程的结构特征选择解题方法.


 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
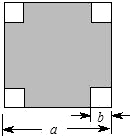 如图,在一块边长为acm的正方形纸板的四角,各剪去一个边长为bcm的正方形(b<$\frac{a}{2}$),列出表示剩余部分面积的代数式,然后利用因式分解计算当a=13.2,b=3.4时,剩余部分的面积.
如图,在一块边长为acm的正方形纸板的四角,各剪去一个边长为bcm的正方形(b<$\frac{a}{2}$),列出表示剩余部分面积的代数式,然后利用因式分解计算当a=13.2,b=3.4时,剩余部分的面积.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
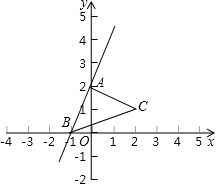 在平面直角坐标系中,点A,B,C的坐标分别为(0,2),(-1,0),(2,1).
在平面直角坐标系中,点A,B,C的坐标分别为(0,2),(-1,0),(2,1).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com