
【题目】如图,已知△ABC,CO⊥AB于O,且CO=8,AB=22,sinA=![]() ,点D为AC的中点,点E为射线OC上任意一点,连结DE,以DE为边在DE的右侧按顺时针方向作正方形DEFG,设OE=x.
,点D为AC的中点,点E为射线OC上任意一点,连结DE,以DE为边在DE的右侧按顺时针方向作正方形DEFG,设OE=x.
(1)求AD的长;
(2)记正方形DEFG的面积为y,① 求y关于x的函数关系式;② 当DF∥AB时,求y的值;
(3)是否存在x的值,使正方形的顶点F或G落在△ABC的边上?若存在,求出所有满足条件的x的值;若不存在,说明理由。
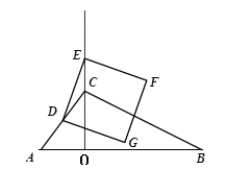
【答案】(1)5;(2)y=(x-4)2+9;18;(3)![]() 或21或3或
或21或3或![]() .
.
【解析】(2)①如图1,过点D作DE⊥y轴于H,则EH=|n-4|,根据正方形的面积公式和勾股定理可得S关于n的函数关系式;
②当DF∥x轴时,点H即为正方形DEFG的中心,可得n=7,再代入函数关系式即可得到S的值;
(3)根据待定系数法可得BC为:y=![]() x+8,再分四种情况:①当点F落在BC上时;②当点G落在BC上时;③当点F落在AB上时;④当点G落在AB上时;
x+8,再分四种情况:①当点F落在BC上时;②当点G落在BC上时;③当点F落在AB上时;④当点G落在AB上时;
矩形讨论可得所有满足条件的n的值.
(1)AD=5
(2)①如图所示,过点D作DH⊥OC于H,

∴y=DE2= EH2 +DH2=(x-4)2+9
②当DF∥AB时,点H即为正方形DEFG的中心
∴EH=DH=3
∴x=4+3=7
∴y=(7-4)2+9=18
(3)①当点F落在BC边上时,如图所示,

由△DEM≌△EFN
得x=![]()
②当点G落在BC边上时,如图所示,
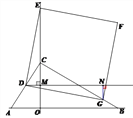
由△DEM≌△GDN
得x=21
③当点F落在AB边上时,如图所示,

由①同理可得△DEM≌△EFO
即x=3
④当点G落在AC边上时,如图所示,
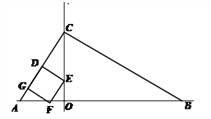
由△DCE∽△OCA
得x=![]()


科目:初中数学 来源: 题型:
【题目】如图,△ABC的顶点坐标分别为A(4,6),B(5,2),C(2,1), 
(1)作出△ABC关于y轴对称的△A′B′C′,并写出A′,B′,C′的坐标.
(2)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的袋子中装有1个白球,2个黄球和3个红球,每个除颜色外完全相同,将球摇匀从中任取一球:(1)恰好取出白球;
(2)恰好取出红球;
(3)恰好取出黄球,
根据你的判断,将这些事件按发生的可能性从小到大的顺序排列 (只需填写序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,AB=AC,D是BC的中点,DE⊥AB于E,DF⊥AC于F,则图中共有全等三角形( ) 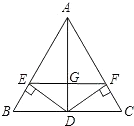
A.5对
B.4对
C.3对
D.2对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“共享单车”逐渐成为人们方便快捷的出行方式,这些单车投入市场后使用者通过扫描车上二维码注册,首次需对该品牌车辆一次性支付一定数额的押金,而后就可以多次使用该品牌的任意一辆单车,按照使用的次数进行付费。2017年无锡市场上主要有“小鸣”单车、“摩拜”单车、hellobike和ofo小黄车。某公司2017年负责运营“小鸣”单车和摩拜单车,在2017年年初一次性投入700万元购买两种单车投入市场,这些单车投入市场后平均每辆车能收到3位不同使用者支付的押金,共收取押金3585万元。这两种单车的成本、每辆车押金、每辆车平均每天使用的次数、每次使用的价格和每种单车年平均使用率如下表所示:
类型 | 成本 (元/辆) | 押金 (元/辆) | 每辆车平均每天使用的次数 | 每次使用的价格(元/次) | 单车年平均使用率 |
“小鸣”单车 | 120 | 199 | 4 | 1 | 60℅ |
“摩拜”单车 | 170 | 299 | 3 | 2 | 50℅ |
(1)求2017年该公司投入市场的“小鸣”单车、“摩拜”单车各多少万辆?
(2)若这些车投入市场后,该公司所收取的押金每年能稳定在3585万元,所收押金每年还能获取15℅的投资收益,但每辆车每年需要投入35元的维护费,公司每年还需要各项支出725万元,每辆单车按照实际使用200天计算,该公司至少几年后能获得不低于8411万元的利润?
(利润=押金投资收益+单车运营收入-维护费-支出-单车成本)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com