
【题目】如图,等边△ABC边长为10,点P是AB边上的一个动点(与点A、B不重合).直线1是经过点P的一条直线,把△ABC沿直线1折叠,点B的对应点是点B′.

(1)如图1,当PB=5时,若点B′恰好在AC边上,求AB′的长度;
(2)如图2,当PB=8时,若直线1∥AC,求BB′的长度;
(3)如图3,点P在AB边上运动过程中,若直线1始终垂直于AC,△ACB′的面积是否变化?若变化,说明理由;若不变化,求出面积.
【答案】(1)5;(2)8![]() ;(3)面积不变,面积为25
;(3)面积不变,面积为25![]()
【解析】
(1)证明△APB′是等边三角形即可解决问题.
(2)如图2中,设直线l交BC于点E.连接BB′交PE于O.证明△PEB是等边三角形,求出OB即可解决问题.
(3)如图3中,结论:面积不变.证明BB′∥AC即可.
(1)如图1中,
∵△ABC是等边三角形,
∴∠A=60°,AB=BC=AC=10,
∵PB=5,
∴PB′=PB=PA=5,
∵∠A=60°,
∴△APB′是等边三角形,
∴AB′=AP=5.
(2)如图2中,设直线l交BC于点E.连接BB′交PE于O.

∵PE∥AC,
∴∠BPE=∠A=60°,∠BEP=∠C=60°,
∴△PEB是等边三角形,
∵PB=8,
∴PB′=PB=8,
∵B,B′关于PE对称,
∴BB′⊥PE,BB′=2OB
∴OB=4![]() ,
,
∴BB′=8![]() .
.
(3)结论:面积不变.
如图3中,连接B'P,BB',
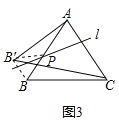
∵B,B′关于直线l对称,
∴BB′⊥直线l,
∵直线l⊥AC,
∴AC∥BB′,
∴S△ACB′=S△ACB=![]() =25
=25![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,使ΔABC≌ΔADC成立的条件是( )

A.AB=AD,∠B=∠DB.AB=AD,∠ACB=ACD
C.BC=DC,∠BAC=∠DACD.AB=AD,∠BAC=∠DAC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,D是AC上一点,E是BD上一点,∠A=∠CBD=∠DCE.
(1)求证:△ABC∽△CDE;
(2)若BD=3DE,试求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们用f(x)表示不大于x的最大整数,例如:f(2.3)=2,f(4)=4,f(﹣1.5)=﹣2;用g(y)表示不小于y的最小整数.例如:g(2.5)=3,g(5)=5,g(﹣3.5)=﹣3.解决下列问题:
(1)根据以上运算规律:f(﹣5.4)=______,g(4.5)=______.
(2)若f(x)=3,则x的取值范围是_______;若g(y)=﹣2,则y的取值范围是______.
(3)已知x,y满足![]() ,求x,y的取值范围.
,求x,y的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D为边BC的中点,过点A作射线AE,过点C作CF⊥AE于点F,过点B作BG⊥AE于点G,连接FD并延长,交BG于点H.
(1)求证:DF=DH;
(2)若∠CFD=120°,求证:△DHG为等边三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠A=90°,AD∥BC,AB=4,点P是线段AD上的动点,连接BP,CP,若△BPC周长的最小值为16,则BC的长为( )

A.5B.6C.8D.10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中每个小方格都是边长为1个单位的正方形,已知△ABC的三个顶点在格点上.
(1)画出△A1B1C1,使它与△ABC关于直线a对称;
(2)求出△A1B1C1的面积;
(3)在直线a上画出点P,使PA+PC最小,最小值为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD的边长是4,点E是AB边上一动点,连接CE,过点B作BG⊥CE于点G,点P是AB边上另一动点,则PD+PG的最小值为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商城销售A,B两种自行车.A型自行车售价为2 100元/辆,B型自行车售价为1 750元/辆,每辆A型自行车的进价比每辆B型自行车的进价多400元,商城用80 000元购进A型自行车的数量与用64 000元购进B型自行车的数量相等.
(1)求每辆A,B两种自行车的进价分别是多少?
(2)现在商城准备一次购进这两种自行车共100辆,设购进A型自行车m辆,这100辆自行车的销售总利润为y元,要求购进B型自行车数量不超过A型自行车数量的2倍,总利润不低于13 000元,求获利最大的方案以及最大利润.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com