
��֪����x��һԪ���η���x2-mx+m-1=0.
(1)��֤:����mȡ�κ�ʵ��ʱ,��������ʵ����;
(2)����x�Ķ��κ���y1=x2-mx+m-1��ͼ��C1����(k-1,k2-6k+8)��(-k+5,k2-6k+8)����.
����������κ����Ľ���ʽ;
�������е�������E��x�ᷭ�ۺ�,������ƽ��2����λ,����ƽ��8����λ�õ�������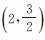 .��������C2��x����M,N����(��M�ڵ�N�����),��P(a,b)Ϊ������C2��x���Ϸ�����ͼ���ϵ�һ������.����MPN��45��ʱ,ֱ��д��a��ȡֵ��Χ.
.��������C2��x����M,N����(��M�ڵ�N�����),��P(a,b)Ϊ������C2��x���Ϸ�����ͼ���ϵ�һ������.����MPN��45��ʱ,ֱ��д��a��ȡֵ��Χ.
 ������״Ԫ��ҵϵ�д�
������״Ԫ��ҵϵ�д� ��ʱ�ƿ�������ϰϵ�д�
��ʱ�ƿ�������ϰϵ�д� һ��һ��һ��ͨϵ�д�
һ��һ��һ��ͨϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����˵����ȷ���ǣ�������
A�����ཻ�������߶���ƽ����
B�����ཻ������ֱ����ƽ����
C�����ཻ������������ƽ����
D����ͬһƽ���ڣ����ཻ������ֱ����ƽ����
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��֪������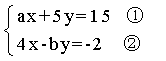 ���ڼ����˷��̢��е�a�õ��ķ�����Ľ�Ϊ
���ڼ����˷��̢��е�a�õ��ķ�����Ľ�Ϊ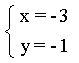 �ҿ����˷��̢��е�b���õ�������Ľ�Ϊ
�ҿ����˷��̢��е�b���õ�������Ľ�Ϊ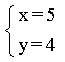 ������ȷ��a��bΪ���㣬��ԭ������Ľ�x��y�IJ
������ȷ��a��bΪ���㣬��ԭ������Ľ�x��y�IJ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��a��b��0�������и�ʽ��һ����ȷ���ǣ� ��
A��a��b B��ab��0 C��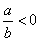 D����a����b
D����a����b
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ͼ�Ǻ���y=x2+bx-1��ͼ��,����ͼ���ṩ����Ϣ,ȷ��ʹ-1��y��2���Ա���x��ȡֵ��Χ����������.
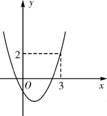
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ͬһֱ������ϵ��,����y=mx+m�ͺ���y=-mx2+2x+2(m�dz���,��m��0)��ͼ�������(����).
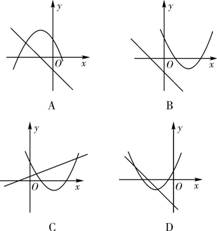
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com