
【题目】(本小题满分11分)如果一个三角形能被一条线段分割成两个等腰三角形,那么称这条线段为这个三角形的特异线,称这个三角形为特异三角形.
(1)如图1,△ABC中,∠B=2∠C,线段AC的垂直平分线交AC于点D,交BC于点E.求证:AE是△ABC的一条特异线;
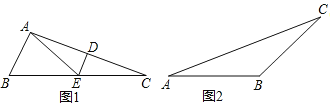
(2)如图2,若△ABC是特异三角形,∠A=30°,∠B为钝角,求出所有可能的∠B的度数.
【答案】见解析
【解析】(1)如图1中,
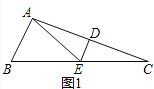
∵DE是线段AC的垂直平分线,∴EA=EC,即△EAC是等腰三角形,(2分)
∴∠EAC=∠C,∴∠AEB=∠EAC+∠C=2∠C,
∵∠B=2∠C,∴∠AEB=∠B,即△EAB是等腰三角形,(4分)
∴AE是△ABC的一条特异线.(5分)
(2)如图2中,
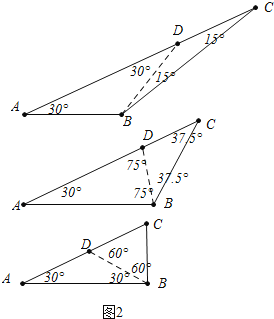
当BD是特异线时,如果AB=BD=DC,则∠ABC=∠ABD+∠DBC=120°+15°=135°,
如果AD=AB,DB=DC,则∠ABC=∠ABD+∠DBC=75°+37.5°=112.5°,
如果AD=DB,DC=CB,则ABC=∠ABD+∠DBC=30°+60°=90°(不合题意,舍去).(8分)
如图3中,当AD是特异线时,AB=BD,AD=DC,则∠ABC=180°–20°–20°=140°,(9分)

当CD为特异线时,不合题意.(10分)
∴符合条件的∠ABC的度数为135°或112.5°或140°.(11分)


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】用一个平面去截一个几何体,其截面形状是圆,则原几何体可能为___________________
①圆柱 ②圆锥 ③球 ④正方体 ⑤长方体(请填上正确的序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,解答问题:
定义:线段AD把等腰三角形ABC分成△ABD与△ACD(如图1),如果△ABD与△ACD均为等腰三角形,那么线段AD叫做△ABC的完美分割线.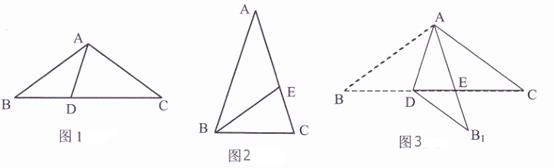
(1)如图1,已知△ABC中,AB=AC,∠BAC=108°,AD为△ABC的完美分割线,且BD<CD,则∠B= , ∠ADC=.
(2)如图2,已知△ABC中,AB=AC,∠A=36°,BE为△ABC的角平分线,求证:BE为△ABC完美分割线.
(3)如图3,已知△ABC是一等腰三角形纸片,AB=AC,AD是它的一条完美分割线,将△ABD沿直线AD折叠后,点B落在点B1处,AB1交CD于点E,求证:DB1=EC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将抛物线y=x2﹣2x+3向上平移2个单位长度,再向右平移3个单位长度后,得到的抛物线的解析式为( )
A.y=(x﹣1)2+4B.y=(x﹣4)2+4C.y=(x+2)2+6D.y=(x﹣4)2+6
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com