
����Ŀ������һ��С�����ڼ䣬ij����Ϊ�������˿ͣ������һ�ִ��������һ�����������������4����ͬ��С�����Ϸֱ���С�0Ԫ������10Ԫ������20Ԫ������30Ԫ�����������涨���˿��ڱ�����һ���Թ�����500Ԫ���Ͼ��ɻ����������Ļ��ᣨ����С���Żأ������и�����С��������ĺͷ�����Ӧ�Ĵ���ȯ��
��1���˿ͼ���1000Ԫ���������ٿɻ��� ��Ԫ����ȯ�����ɻ��� ��Ԫ����ȯ��
��2����������ͼ���б�����������˿ͼ�ò�����30Ԫ����30Ԫ������ȯ�ĸ��ʣ�
���𰸡���1��0��60����2��ͼ��������![]() ��
��
��������
��1�����ٵõ��Ľ����Ϊ0+0��0Ԫ������õ��Ľ����Ϊ30+30��60Ԫ��
��2���оٳ�������������ù˿�����ù���ȯ�Ľ�����30Ԫ�������ռ��������Ķ��ټ��ɣ�
�⣺��1�����ٵõ��Ľ����Ϊ0+0��0Ԫ������õ��Ľ����Ϊ30+30��60Ԫ��
�ʴ�Ϊ0��60��
��2������״ͼ���£�
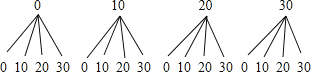
��16�������������30Ԫ���������10�֣�
��������ĸ���Ϊ![]() ��
��![]() ��
��


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
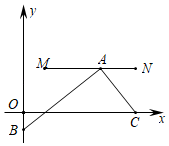
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�M��N��C���������ֱ�Ϊ��![]() ��1������3��1������3��0������AΪ�߶�MN�ϵ�һ�����㣬����AC������A��AB��AC��y���ڵ�B������A��M�˶���Nʱ����B��֮�˶������B������Ϊ��0��b������b��ȡֵ��Χ�ǣ�������
��1������3��1������3��0������AΪ�߶�MN�ϵ�һ�����㣬����AC������A��AB��AC��y���ڵ�B������A��M�˶���Nʱ����B��֮�˶������B������Ϊ��0��b������b��ȡֵ��Χ�ǣ�������
A.![]() ��b��1B.
��b��1B.![]() ��b��1C.
��b��1C.![]() ��b��
��b��![]() D.
D.![]() ��b��1
��b��1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB�ǡ�O��ֱ����AC�ǡ�O���ң���BAC��ƽ���߽���O�ڵ�D������D��DE��AC��AC���ӳ����ڵ�E������BD��
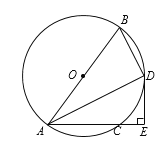
��1����֤��DE�ǡ�O�����ߣ�
��2����BD��3��AD��4����DE�� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����壺��ƽ��ֱ������ϵ�У�������������![]() ��
��![]() ������
������![]() ����
����![]() ��
��![]() ����ô�Ƶ�
����ô�Ƶ�![]() �ǵ�
�ǵ�![]() ��
��![]() ���ںϵ�.
���ںϵ�.
���磺![]() ��
��![]() ������
������![]() ����
����![]() ��
��![]() ʱ�����
ʱ�����![]() �ǵ�
�ǵ�![]() ��
��![]() ���ںϵ㣬
���ںϵ㣬

��1����֪��![]() ��
��![]() ��
��![]() ����˵������һ������������������ںϵ�.
����˵������һ������������������ںϵ�.
��2����ͼ����![]() ����
����![]() ��ֱ��
��ֱ��![]() ������һ�㣬��
������һ�㣬��![]() �ǵ�
�ǵ�![]() ��
��![]() ���ںϵ�.
���ںϵ�.
����ȷ��![]() ��
��![]() �Ĺ�ϵʽ.
�Ĺ�ϵʽ.
����ֱ��![]() ��
��![]() ���ڵ�
���ڵ�![]() ����
����![]() Ϊֱ��������ʱ�����
Ϊֱ��������ʱ�����![]() ������.
������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
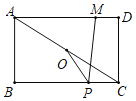
����Ŀ����ͼ���ھ���ABCD�У�AB��3��AD��4������AC��O��AC���е㣬M��AD��һ�㣬��MD��1��P��BC��һ���㣬��PM��PO�����ֵΪ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
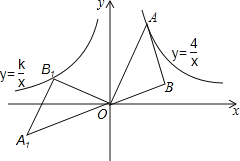
����Ŀ����ͼ��A�Ƿ���������y��![]() ��x��0��ͼ����һ�㣬��OAΪб��������ֱ�ǡ�ABO������ABO�Ƶ�O����ʱ����ת135�����õ���A1B1O��������������y��
��x��0��ͼ����һ�㣬��OAΪб��������ֱ�ǡ�ABO������ABO�Ƶ�O����ʱ����ת135�����õ���A1B1O��������������y��![]() ��ͼ����B1����k��ֵ��_____��
��ͼ����B1����k��ֵ��_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() ��a��0����x����A��B���㣬A������Ϊ��3��0������y�ύ�ڵ�C��0��4������OC��OAΪ��������OADC���������ڵ�G��
��a��0����x����A��B���㣬A������Ϊ��3��0������y�ύ�ڵ�C��0��4������OC��OAΪ��������OADC���������ڵ�G��
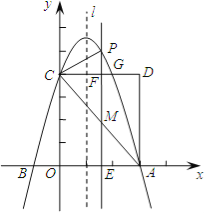
��1���������ߵĽ���ʽ��
��2�������ߵĶԳ���l�ڱ�OA��������O��A���㣩��ƽ���ƶ����ֱ�x���ڵ�E����CD�ڵ�F����AC�ڵ�M�����������ڵ�P������M�ĺ�����Ϊm�����ú�m�Ĵ���ʽ��ʾPM�ij���
��3���ڣ�2���������£�����PC������CD�Ϸ��������߲����Ƿ���������ĵ�P��ʹ����P��C��FΪ����������κ���AEM���ƣ������ڣ������ʱm��ֵ����ֱ���ж���PCM����״���������ڣ���˵��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
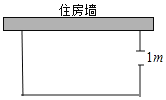
����Ŀ����ͼ��һũ��Ҫ��һ���������ᣬ�����һ�����ó�Ϊ15m��ס��ǽ������������27m���Ľ�������Χ�ɣ�Ϊ����������ڴ�ֱ��ס��ǽ��һ����һ��1m�����ţ���Χ��������ij������ֱ�Ϊ������ʱ���������Ϊ96m2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����O�У�ֱ��CD����AB��E��AM��BC��M����CD��N������AD��
��AD_____AN������������������������������
��AB��8��ON��1����O�İ뾶Ϊ_____��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com