
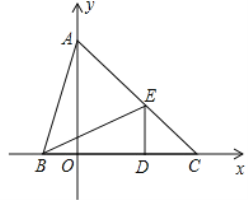
【题目】如图,在平面直角坐标系中,点A(0,b),点B(a,0),点D(2,0),其中a、b满足![]() , DE⊥x轴,且∠BED=∠ABO,直线AE交x轴于点C.
, DE⊥x轴,且∠BED=∠ABO,直线AE交x轴于点C.
(1)求A、B、E三点的坐标;
(2) 若以AB为一边在第二象限内构造等腰直角三角形△ABF,请直接写出点F的坐标.
【答案】(1)A(0,3),B(-1,0),E(2,1),(2) (-4,1)(-3,4)(-2,2)
【解析】
(1)先根据非负数的性质求出a、b的值,进而可得出A、B两点的坐标;由已知角相等,加上一对直角相等,且根据A,B与D的坐标确定出OA=BD,利用AAS得到△AOB与△BED全等,利用全等三角形的对应边相等得到OB=ED,进而确定出E坐标.
(2)分∠BAF=90°,∠ABF=90°或∠AFB=90°三种情况进行讨论.
解:(1)∵a、b满足![]() +|b-3|=0,
+|b-3|=0,
∴a+1=0,b-3=0,解得a=-1,b=3,
∵A(0,3),B(-1,0);
(2)∵B(-1,0),D(2,0),A(0,3),
∴OB=1,OD=2,即BD=OB+OD=1+2=3,
∴OA=BD=3,
在△ABO和△BED中,
∠AOB=∠BDE=90°,
∠ABO=∠BEO,
OA=BD,
∴△ABO≌△BED(AAS),
∴ED=OB=1,
∴E(2,1).
(2)如图所示,当∠BAF=90°时,

过点F1作F1G⊥y轴于点G,
∵∠F1AG+∠AF1G=90°,∠F1AG+∠BAO=90°,
∴∠AF1G=∠BAO,
在△AGF1与△BOA中,
∠AF1G=∠BAO,
∠AGF1=∠BOA,
AF1=AB,
∴△AGF1≌△BOA,
∴AG=OB=1,GF1=OA=3,
∴F1(-3,4);
当∠ABF=90°时,过点F2作F2G⊥x轴于点H,
同理可得△OAB≌△HBF2,
∴BH=OA=3,F2H=OB=1,
∴OH=BH+OB=3+1=4,
∴F2(-4,1);
当∠AFB=90°时,设直线AB的解析式为y=kx+b(k≠0),
∵A(0,3),B(-1,0),
∴![]() ,解得
,解得![]() ,
,
∴直线AB的解析式为y=3x+3.
设线段AB的中点为M,则M(-![]() ,
,![]() ),
),
设线段AB的垂直平分线l的解析式为y=-![]() x+c(a≠0),
x+c(a≠0),
∴![]() +c=
+c=![]() ,解得c=
,解得c=![]() ,
,
∴直线l的解析式为y=-![]() x+
x+![]() .
.
设F3(x,-![]() x+
x+![]() ),
),
∵△AF3B是等腰直角三角形,AB=![]() =
=![]() ,
,
∴AF3=![]() ,
,
∴x2+(-![]() x+
x+![]() -3)2=5,解得x=-1,
-3)2=5,解得x=-1,
∴F3(-1,2).
综上所述,F点的坐标为(-3,4)或(-4,1)或(-1,2).


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,长方形OABC中,O为平面直角坐标系的原点,A点的坐标为![]() ,C点的坐标为
,C点的坐标为![]() ,点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着
,点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着![]() 的路线移动
的路线移动![]() 即:沿着长方形移动一周
即:沿着长方形移动一周![]() .
.
![]() 写出点B的坐标
写出点B的坐标![]() ______
______![]()
![]() 当点P移动了4秒时,描出此时P点的位置,并求出点P的坐标.
当点P移动了4秒时,描出此时P点的位置,并求出点P的坐标.
![]() 在移动过程中,当点P到x轴距离为5个单位长度时,求点P移动的时间.
在移动过程中,当点P到x轴距离为5个单位长度时,求点P移动的时间.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了丰富学生的课外活动,某校决定购买100个篮球和![]() 副羽毛球拍.经调查发现:甲、乙两个体育用品商店以同样的价格出售同种品牌的篮球和羽毛球拍.已知每个篮球比每副羽毛球拍贵25元,两个篮球与三副羽毛球拍的费用正好相等.经洽谈,甲商店的优惠方案是:每购买十个篮球,送一副羽毛球拍;乙商店的优惠方案是:若购买篮球数超过80个,则购买羽毛球拍可打八折.
副羽毛球拍.经调查发现:甲、乙两个体育用品商店以同样的价格出售同种品牌的篮球和羽毛球拍.已知每个篮球比每副羽毛球拍贵25元,两个篮球与三副羽毛球拍的费用正好相等.经洽谈,甲商店的优惠方案是:每购买十个篮球,送一副羽毛球拍;乙商店的优惠方案是:若购买篮球数超过80个,则购买羽毛球拍可打八折.
(1)求每个篮球和每副羽毛球拍的价格分别是多少?
(2)请用含![]() 的代数式分别表示出到甲商店和乙商店购买所花的费用;
的代数式分别表示出到甲商店和乙商店购买所花的费用;
(3)请你决策:在哪家商店购买划算?(直接写出结论)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy,直线y=x﹣1与y轴交于点A,与双曲线y= ![]() 交于点B(m,2)
交于点B(m,2) 
(1)求点B的坐标及k的值;
(2)将直线AB平移,使它与x轴交于点C,与y轴交于点D,若△ABC的面积为6,求直线CD的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB,CD相交于点O,OE⊥AB于O,若∠BOD=40°,则不正确的结论是( )

A.∠AOC=40° B.∠COE=130° C.∠EOD=40° D.∠BOE=90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是小强洗漱时的侧面示意图,洗漱台(矩形 ![]() )靠墙摆放,高
)靠墙摆放,高 ![]() ,宽
,宽 ![]() ,小强身高
,小强身高 ![]() ,下半身
,下半身 ![]() ,洗漱时下半身与地面成
,洗漱时下半身与地面成 ![]() (
( ![]() ),身体前倾成
),身体前倾成 ![]() (
( ![]() ),脚与洗漱台距离
),脚与洗漱台距离 ![]() (点
(点 ![]() ,
, ![]() ,
, ![]() ,
, ![]() 在同一直线上).
在同一直线上).
(1)此时小强头部 ![]() 点与地面
点与地面 ![]() 相距多少?
相距多少?
(2)小强希望他的头部 ![]() 恰好在洗漱盆
恰好在洗漱盆 ![]() 的中点
的中点 ![]() 的正上方,他应向前或后退多少?
的正上方,他应向前或后退多少?
( ![]() ,
, ![]() ,
, ![]() ,结果精确到
,结果精确到 ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形OABC中,O为平面直角坐标系的原点,A点的坐标为(4,0),C点的坐标为(0,6),点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着O﹣C﹣B﹣A﹣O的路线移动(即:沿着长方形移动一周). 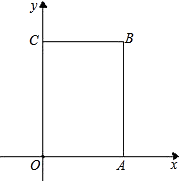
(1)写出B点的坐标();
(2)当点P移动了4秒时,描出此时P点的位置,并写出点P的坐标.
(3)在移动过程中,当点P到x轴距离为5个单位长度时,求点P移动的时间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com