
【题目】如图,已知抛物线与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() .
.

(1)求抛物线的解析式;
(2)点![]() 是第一象限内抛物线上的一个动点(与点
是第一象限内抛物线上的一个动点(与点![]() 、
、![]() 不重合),过点
不重合),过点![]() 作
作![]() 轴于点
轴于点![]() ,交直线
,交直线![]() 于点
于点![]() ,连接
,连接![]() 、
、![]() .设点
.设点![]() 的横坐标为
的横坐标为![]() ,
,![]() 的面积为
的面积为![]() .求
.求![]() 关于
关于![]() 的函数解析式及自变量
的函数解析式及自变量![]() 的取值范围,并求出
的取值范围,并求出![]() 的最大值;
的最大值;
(3)已知![]() 为抛物线对称轴上一动点,若
为抛物线对称轴上一动点,若![]() 是以
是以![]() 为直角边的直角三角形,请直接写出点
为直角边的直角三角形,请直接写出点![]() 的坐标.
的坐标.
【答案】(1)![]() ;(2)
;(2)![]() ,当
,当![]() 时,
时,![]() 有最大值,最大值
有最大值,最大值![]() ;(3)
;(3)![]() ,
,![]()
【解析】
(1)由抛物线与x轴的两个交点坐标可设抛物线的解析式为y=a(x+1)(x-3),将点C(0,3)代入抛物线解析式中即可得出关于a一元一次方程,解方程即可求出a的值,从而得出抛物线的解析式;
(2)设直线BC的函数解析式为y=kx+b.结合点B、点C的坐标利用待定系数法求出直线BC的函数解析式,再由点D横坐标为m找出点D、点E的坐标,结合两点间的距离公式以及三角形的面积公式求出函数解析式,利用配方法将S关于m的函数关系式进行变形,从而得出结论;
(3)先求出对称轴,设M(1,y),然后分分BM为斜边和CM为斜边两种情况求解即可;
解:(1)∵抛物线与x轴交于A(-1,0)、B(3,0)两点,
∴设抛物线的解析式为y=a(x+1)(x-3),
又∵点C(0,3)在抛物线图象上,
∴3=a×(0+1)×(0-3),解得:a=-1.
∴抛物线解析式为y=-(x+1)(x-3)=-x2+2x+3.
∴抛物线解析式为![]() ;
;
(2)设直线![]() 的函数解析式为
的函数解析式为![]() ,
,
∵直线![]() 过点
过点![]() ,
,![]() ,
,
∴![]() ,解得
,解得![]() ,
,
∴![]() ,
,
设![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴当![]() 时,
时,![]() 有最大值,最大值
有最大值,最大值![]() ;
;
(3)∵![]() ,
,
∴对称轴为直线x=1,
设M(1,y),
则CM2=1+(y-3)2=y2-6y+10,
BM2=y2+(1-3)2=y2+4,
BC2=9+9=18.
当BM为斜边时,
则y2-6y+10+18= y2+4,
解得
y=4,
此时M(1,4);
当CM为斜边时,
y2+4+18= y2-6y+10,
解得
y=-2,
此时M(1,-2);
综上可得点![]() 的坐标为
的坐标为![]() ,
,![]() .
.


 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案科目:初中数学 来源: 题型:
【题目】汽车刹车后,还会继续向前滑行一段距离,这段距离称为“刹车距离”刹车距离y(m)与刹车时的车速x(km/h)的部分关系如表:
刹车时的车速 | 0 | 50 | 100 | 150 | 200 |
刹车距离 | 0 | 5.5 | 21 | 46.5 | 82 |
(1)求出y与x之间的函数关系式.
(2)一辆车在限速120km/h的高速公路上行驶时出了事故,事后测得它的刹车距离为40.6m,问:该车在发生事故时是否超速行驶?
查看答案和解析>>
科目:初中数学 来源: 题型:
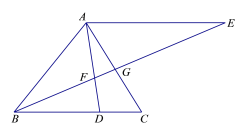
【题目】已知:如图,在△ABC中,点D在边BC上,AE∥BC,BE与AD、AC分别相交于点F、G, ![]() .
.
(1)求证:△CAD∽△CBG;
(2)联结DG,求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
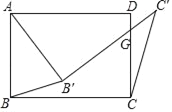
【题目】如图,在矩形ABCD中,将∠ABC绕点A按逆时针方向旋转一定角度后,BC的对应边B'C'交CD边于点G.连接BB'、CC'.若AD=7,CG=4,AB'=B'G,则![]()
=__(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】消费者在某火锅店饭后买单时可以参与一个抽奖游戏,规则如下:有![]() 张纸牌,它们的背面都是小猪佩奇头像,正面为
张纸牌,它们的背面都是小猪佩奇头像,正面为![]() 张笑脸、
张笑脸、![]() 张哭脸.现将
张哭脸.现将![]() 张纸牌洗匀后背面朝上摆放到桌上,然后让消费者去翻纸牌.
张纸牌洗匀后背面朝上摆放到桌上,然后让消费者去翻纸牌.
(1)现小杨有一次翻牌机会,若正面是笑脸的就获奖,正面是哭脸的不获奖,她从中随机翻开一张纸牌,小杨获奖的概率是________.
(2)如粜小杨、小月都有翻两张牌的机会,小杨先翻一张,放回后再翻一张;小月同时翻开两张纸牌.他们翻开的两张纸牌中只要出现一张笑脸就获奖.他们谁获奖的机会更大些?通过画树状图或列表法分析说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:方程cx2+bx+a=0是一元二次方程ax2+bx+c=0的倒方程.
(1)已知x=2是x2+2x+c=0的倒方程的解,求c的值;
(2)若一元二次方程ax2﹣2x+c=0无解,求证:它的倒方程也一定无解;
(3)一元二次方程ax2﹣2x+c=0(a≠c)与它的倒方程只有一个公共解,它的倒方程只有一个解,求a和c的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BD是平行四边形ABCD的对角线,DE⊥AB于点E,过点E的直线交BC于点G,且BG=CG.
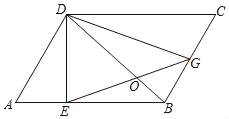
(1)求证:GD=EG.
(2)若BD⊥EG垂足为O,BO=2,DO=4,画出图形并求出四边形ABCD的面积.
(3)在(2)的条件下,以O为旋转中心顺时针旋转△GDO,得到△G′D'O,点G′落在BC上时,请直接写出G′E的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 经过
经过![]() ,
,![]() 两点,与y轴交于点C,连接AB,AC,BC.
两点,与y轴交于点C,连接AB,AC,BC.

![]() 求抛物线的表达式;
求抛物线的表达式;
![]() 求证:AB平分
求证:AB平分![]() ;
;
![]() 抛物线的对称轴上是否存在点M,使得
抛物线的对称轴上是否存在点M,使得![]() 是以AB为直角边的直角三角形,若存在,求出点M的坐标;若不存在,请说明理由.
是以AB为直角边的直角三角形,若存在,求出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
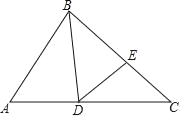
【题目】如图,BD是△ABC的角平分线,点E位于边BC上,已知BD是BA与BE的比例中项.
(1)求证:∠CDE=![]() ∠ABC;
∠ABC;
(2)求证:ADCD=ABCE.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com