
分析 (1)增长率的问题,用解增长率问题的模型解答;
(2)根据两种车位数量是未知数,建立等式和不等式两种关系,而车位数为整数,变无数解为有限解.
解答 解:(1)设家庭轿车拥有量的年平均增长率为x,
则64(1+x)2=100
解得x=$\frac{1}{4}$=25%,或x=-$\frac{9}{4}$(不合题意,舍去)
∴100(1+25%)=125
答:该小区到2014年底家庭轿车将达到125辆;
(2)设该小区可建室内车位a个,露天车位b个,
则$\left\{\begin{array}{l}{0.5a+0.1b=15}\\{2a≤b≤2.5a}\end{array}\right.$,
由①得b=150-5a
代入②得20≤a≤$\frac{150}{7}$,
∵a是正整数
∴a=20或21
当a=20时b=50,当a=21时b=45.
∴方案一:建室内车位20个,露天车位50个;
方案二:室内车位21个,露天车位45个.
点评 考查了一元二次方程的应用及一元一次不等式组的应用,解答综合题,需要由浅入深,认真读题,理解题意,合理设未知数,分步解答.


科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (x+3)2=8 | B. | (x-3)2=8 | C. | (x-3)2=10 | D. | (x+3)2=10 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
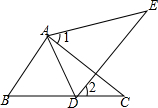 如图,点D在BC上,∠1=∠2,AE=AC,下面三个条件:①AB=AD;②BC=DE;③∠E=∠C,请你从所给条件①②③中选一个条件,使△ABC≌△ADE,并证明两三角形全等.
如图,点D在BC上,∠1=∠2,AE=AC,下面三个条件:①AB=AD;②BC=DE;③∠E=∠C,请你从所给条件①②③中选一个条件,使△ABC≌△ADE,并证明两三角形全等.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| x | … | -4 | -2 | 0 | 2 | 4 | … |
| y | … | -4 | -1 | 0 | -1 | -4 | … |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com