
 ABC考王全优卷系列答案
ABC考王全优卷系列答案科目:初中数学 来源: 题型:选择题
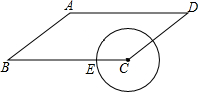 如图,已知在平行四边形ABCD中,AB=5,BC=8,cosB=$\frac{4}{5}$,点E是BC边上的动点,当以CE为半径的⊙C与边AD有两个交点时,半径CE的取值范围是( )
如图,已知在平行四边形ABCD中,AB=5,BC=8,cosB=$\frac{4}{5}$,点E是BC边上的动点,当以CE为半径的⊙C与边AD有两个交点时,半径CE的取值范围是( )| A. | 0<CE≤8 | B. | 0<CE≤5 | C. | 3<CE≤8 | D. | 3<CE≤5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
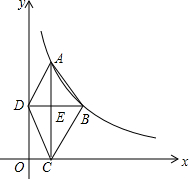 如图所示,反比例函数y=$\frac{k}{x}$(x>0,k>0)的图象经过点A(1,4)和点B(a,b),其中a>1,过点A作x轴的垂线,垂点为C,过点B作y轴的垂线,垂足为D,AC与BD相交于点E,连接AD,DC,CB.
如图所示,反比例函数y=$\frac{k}{x}$(x>0,k>0)的图象经过点A(1,4)和点B(a,b),其中a>1,过点A作x轴的垂线,垂点为C,过点B作y轴的垂线,垂足为D,AC与BD相交于点E,连接AD,DC,CB.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
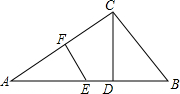 如图,在Rt△ABC中,∠ACB=90°,AF=4,EF⊥AC交AB于E,CD⊥AB,垂足为D.若CD=4,EF=3.则ED=$\frac{1}{3}$,BC=5,AB=$\frac{25}{3}$.
如图,在Rt△ABC中,∠ACB=90°,AF=4,EF⊥AC交AB于E,CD⊥AB,垂足为D.若CD=4,EF=3.则ED=$\frac{1}{3}$,BC=5,AB=$\frac{25}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 方差反映了一组数据的分散或波动的程度 | |
| B. | 数据1,5,3,7,10的中位数是3 | |
| C. | 任何一组数据的平均数和众数都不相等 | |
| D. | 调查一批灯泡的使用寿命适合用全面调查方式 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com