
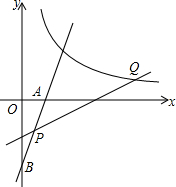
 如图,直线l:y=kx-2k交坐标轴于A,B两点,点P(m,n)为直线l上的一点,且满足关系式2m2+2n2-4m+8n+10=0.
如图,直线l:y=kx-2k交坐标轴于A,B两点,点P(m,n)为直线l上的一点,且满足关系式2m2+2n2-4m+8n+10=0.分析 (1)方程整理后得(m-1)2+(n+2)2=0,即可求得m=1,n=-2,得出P的坐标,代入y=kx-2k即可求得k的值;
(2)作BC⊥AB,交CQ于C,作CD⊥y轴于D,由直线l:y=2x-4可知:A(2,0),B(0,-4),根据勾股定理求得AB=2$\sqrt{5}$,PB=$\sqrt{5}$,从而求得sin∠ABO=sin∠BCD=$\frac{\sqrt{5}}{5}$,cos∠ABO=cos∠BCD=$\frac{2\sqrt{5}}{5}$,进而求得C的坐标,然后利用待定系数法求得直线PQ的解析式,然后与反比例函数的解析式联立方程即可求得Q的坐标.
解答 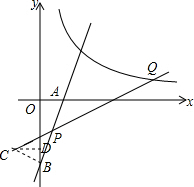 解:(1)方程2m2+2n2-4m+8n+10=0整理得:
解:(1)方程2m2+2n2-4m+8n+10=0整理得:
(m-1)2+(n+2)2=0,
∴m=1,n=-2,
∴P(1,-2),
∵点P(m,n)为直线l上的一点,
∴-2=k-2k,解得k=2;
(2)由直线l:y=2x-4可知:A(2,0),B(0,-4),
∴AB=$\sqrt{{2}^{2}+{4}^{2}}$=2$\sqrt{5}$,
∴sin∠ABO=$\frac{OA}{AB}$=$\frac{2}{2\sqrt{5}}$=$\frac{\sqrt{5}}{5}$,cos∠ABO=$\frac{OB}{AB}$=$\frac{4}{2\sqrt{5}}$=$\frac{2\sqrt{5}}{5}$,
作BC⊥AB,交CQ于C,作CD⊥y轴于D,
∵∠BCD=∠ABO,
∴sin∠BCD=$\frac{\sqrt{5}}{5}$,cos∠BCD=$\frac{2\sqrt{5}}{5}$,
∵PB=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$,∠BPC=∠APQ=45°,
∴BC=PB=$\sqrt{5}$,
∴sin∠BCD=$\frac{BD}{BC}$=$\frac{\sqrt{5}}{5}$,cos∠BCD=$\frac{CD}{BC}$=$\frac{2\sqrt{5}}{5}$,
∴BD=1,CD=2,
∴C(-2,-3),
设直线PQ的解析式为y=ax+b,
∴$\left\{\begin{array}{l}{a+b=-2}\\{-2a+b=-3}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=\frac{1}{3}}\\{b=-\frac{7}{3}}\end{array}\right.$,
∴直线PQ的解析式为y=$\frac{1}{3}$x-$\frac{7}{3}$,
解$\left\{\begin{array}{l}{y=\frac{1}{3}x-\frac{7}{3}}\\{y=\frac{10}{x}}\end{array}\right.$得$\left\{\begin{array}{l}{{x}_{1}=10}\\{{y}_{2}=1}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=-3}\\{{y}_{2}=-\frac{10}{3}}\end{array}\right.$,
∵x>0,
∴Q(10,1).
点评 本题考查了反比例函数与一次函数的交点问题,同时考查了利用待定系数法求反比例函数、一次函数的解析式,锐角三角函数的定义,本题有一定难度.准确作出辅助线利用数形结合是解决(2)的关键.


 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:初中数学 来源: 题型:选择题
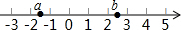 实数a、b在数轴上的位置如图,则化简$\sqrt{{a}^{2}}$+$\sqrt{{b}^{2}}$-$\sqrt{(a-b)^{2}}$的结果是( )
实数a、b在数轴上的位置如图,则化简$\sqrt{{a}^{2}}$+$\sqrt{{b}^{2}}$-$\sqrt{(a-b)^{2}}$的结果是( )| A. | 0 | B. | -2a | C. | 2b | D. | -2a+2b |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
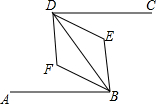 如图,已知AB∥DC,BF平分∠ABE,且BF∥DE,则∠ABE与∠CDE的关系是( )
如图,已知AB∥DC,BF平分∠ABE,且BF∥DE,则∠ABE与∠CDE的关系是( )| A. | ∠ABE=2∠CDE | B. | ∠ABE=3∠CDE | C. | ∠ABE=∠CDE+90° | D. | ∠ABE+∠CDE=180° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com