
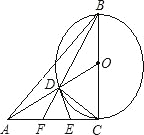
【题目】如图,在△ABC中AC=BC,∠ACB=90°,以BC为直径作⊙O,连接OA,交⊙O于点D,过D点作⊙O的切线交AC于点E,连接B、D并延长交AC于点F.则下列结论错误的是( )
A. △ADE∽△ACO B. △AOC∽△BFC
C. △DEF∽△DOC D. CD2=DFDB
【答案】B
【解析】
根据相似三角形的判定定理,对各选项的三角形进行分析证明,然后利用排除法求解.
解:A、∵DE是⊙O的切线,
∴∠ADE=90°,
∵∠ACB=90°,
∴∠ADE=∠ACB,
∵∠DAE=∠CAO,
∴△ADE∽△ACO;
故本选项正确;
B、假设△AOC∽△BFC,
则有∠OAC=∠FBC,
∵∠ACB=90°,以BC为直径作⊙O,
∴AC是⊙O的切线,
∴∠ACD=∠FBC,
∵∠ODC=∠OAC+∠ACD=2∠OAC,∠COD=2∠FBC,
∴∠ODC=∠COD,
∴OC=CD,
又∵OD=OC,
∴OC=CD=OD,
即△OCD是等边三角形,∠AOC=60°,
∴AC=![]() OC①,
OC①,
而在△ABC中,AC=BC,BC=2OC,
∴AC=2OC②,
∴假设与题目条件相矛盾,
故假设不成立,所以△AOC与△BFC不相似;
故本选项错误;
C、∵∠ACB=90°,
∴∠CBD+∠BFC=90°,
∴BC是⊙O的直径,
∴∠CBD+∠BCD=90°,
∴∠BCD=∠BFC,
∵DE是⊙O的切线,AC是⊙O的切线,
∴∠CDE=∠CED=∠CBD,
又∵∠AED=∠CDE+∠CED=2∠CBD,
∠COD=2∠CBD,
∴∠AED=∠COD,
在△DEF∽△DOC中,
![]() ,
,
∴△DEF∽△DOC,
故本选项正确;
D、∵BC为⊙O的直径,
∴∠CDB=90°,
∴CD⊥BF,
∵∠ACB=90°,
∴CD2=DFDB,
故本选项正确.
故选:B.


科目:初中数学 来源: 题型:
【题目】已知,如图,在△ABC中,∠A=∠ABC,直线EF分别交△ABC的边AB,AC和CB的延长线于点D,E,F.

(1)求证:∠F+∠FEC=2∠A;
(2)过B点作BM∥AC交FD于点M,试探究∠MBC与∠F+∠FEC的数量关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某日上午![]() 点钟,
点钟,![]() 市气象局测得在城市正东方向
市气象局测得在城市正东方向![]() 处
处![]() 点有一台风中心正在以
点有一台风中心正在以![]() 千米/时的速度沿西偏北
千米/时的速度沿西偏北![]() 的
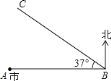
的![]() 方向迅速移动(如图所示).据资料表明,在距离台风中心
方向迅速移动(如图所示).据资料表明,在距离台风中心![]() 范围内为严重影响区域(假定台风中心移动方向不变,影响力不变).(参考数据:
范围内为严重影响区域(假定台风中心移动方向不变,影响力不变).(参考数据:![]() ,
,![]() ).
).
(1)![]() 市会不会受这次台风的严重影响,为什么;
市会不会受这次台风的严重影响,为什么;
(2)如果![]() 市会受严重影响,那么这次台风对
市会受严重影响,那么这次台风对![]() 市严重影响多长时间?
市严重影响多长时间?
(3)![]() 市规定台风严重影响前一小时向市民发出预警警报.如果
市规定台风严重影响前一小时向市民发出预警警报.如果![]() 市会受这次台风严重影响,那么
市会受这次台风严重影响,那么![]() 市应在几点钟发出预警警报?
市应在几点钟发出预警警报?
查看答案和解析>>
科目:初中数学 来源: 题型:
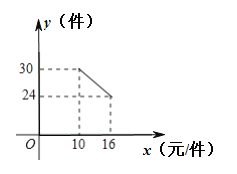
【题目】一名在校大学生利用“互联网+”自主创业,销售一种产品,这种产品成本价10元/件,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于16元/件,市场调查发现,该产品每天的销售量y(件)与销售价x(元/件)之间的函数关系如图所示.
(1)求y与x之间的函数关系式,并写出自变量x的取值范围;
(2)求每天的销售利润W(元)与销售价x(元/件)之间的函数关系式,并求出每件销售价为多少元时,每天的销售利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
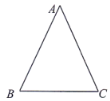
【题目】求证:等腰三角形两腰上的中线相等.
(1)请用尺规作出△ABC两腰上的中线BD、CE(保留痕迹,不写作法);
(2)结合图形,写出已知、求证和证明过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
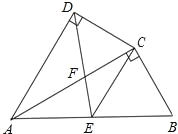
【题目】如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点,
(1)求证:AC2=ABAD;
(2)求证:△AFD∽△CFE.
查看答案和解析>>
科目:初中数学 来源: 题型:
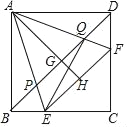
【题目】如图,正方形ABCD的边长为10,点E、F分别在边BC、CD上,且∠EAF=45°,AH⊥EF于点H,AH=10,连接BD,分别交AE、AH、AF于点P、G、Q.
(1)求△CEF的周长;
(2)若E是BC的中点,求证:CF=2DF;
(3)连接QE,求证:AQ=EQ.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列函数关系中,![]() 随
随![]() 的增大而减小的是( )
的增大而减小的是( )
A.长方形的长一定时,其面积![]() 与宽
与宽![]() 的函数关系
的函数关系
B.高速公路上匀速行驶的汽车,其行驶的路程![]() 与行驶时间
与行驶时间![]() 的函数关系
的函数关系
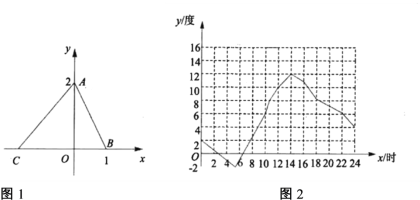
C.如图1,在平面直角坐标系中,点![]() 、
、![]() ,
,![]() 的面积
的面积![]() 与点
与点![]() 的横坐标
的横坐标![]() 的函数关系
的函数关系
D.如图2,我市某一天的气温![]() (度)与时间
(度)与时间![]() (时)的函数关系
(时)的函数关系
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=﹣x2+ ![]() 与y轴相交于点A,点B与点O关于点A对称.
与y轴相交于点A,点B与点O关于点A对称.
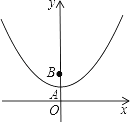
(1)填空:点B的坐标为________;
(2)过点B的直线y=kx+b(其中k<0)与x轴相交于点C,过点C作直线l平行于y轴,P是直线l上一点,且PB=PC,求线段PB的长(用含k的式子表示),并判断点P是否在抛物线上,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com