
【题目】在等边三角形ABC中,点P在△ABC内,点Q在△ABC外,且∠ABP=∠ACQ,BP=CQ. 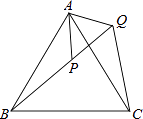
(1)求证:△ABP≌△CAQ;
(2)请判断△APQ是什么形状的三角形?试说明你的结论.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】计算。
(1)你发现了吗?( ![]() )2=
)2= ![]() ×
× ![]() ,(
,( ![]() )﹣2=
)﹣2= ![]() =
= ![]() ×
× ![]() =
= ![]() ×
× ![]() 由上述计算,我们发现(
由上述计算,我们发现( ![]() )2(
)2( ![]() )﹣2;
)﹣2;
(2)仿照(1),请你通过计算,判断( ![]() )3与(
)3与( ![]() )﹣3之间的关系.
)﹣3之间的关系.
(3)我们可以发现:( ![]() )﹣m(
)﹣m( ![]() )m(ab≠0)
)m(ab≠0)
(4)计算:( ![]() )﹣4×(
)﹣4×( ![]() )4 .
)4 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据统计,2017年高新技术产品出口总额达50570亿元,将数据50570亿用科学记数法表示为( )
A.5.0570×109
B.0.50570×1010
C.50.570×1011
D.5.0570×1012
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角三角形ABC中,∠ACB=90°,将△ABC绕点C逆时针方向旋转,使点A落在AB边上的点D处,得到△DEC.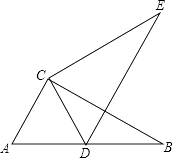
(1)点B的对应点是点 , BC的对应线段是 .
(2)判断△ACD的形状.
(3)若AD=CD,求∠B和∠BCE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国古代数学的许多发现都曾位居世界前列,其中“杨辉三角”(如图所示)就是一例. 
这个三角形的构造法则为:两腰上的数都是1,其余每个数均为其上方左右两数之和.事实上,这个三角形给出了(a+b)n(n为正整数)的展开式(按a的次数由大到小的顺序排列)的系数规律.例如,在三角形中第三行的三个数1,2,1,恰好对应(a+b)2=a2+ab+b2展开式中各项的系数;第四行的四个数1,3,3,1,恰好对应着(a+b)3=a3+3a2b+3ab2+b3展开式中各项的系数等等.根据上面的规律,(a+b)4的展开式中各项系数最大的数为( )
A.4
B.5
C.6
D.7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把四张形状大小完全相同的小长方形卡片(如图①)不重叠地放在一个底面为长方形(长为m,宽为n )的盒子底部(如图②),盒子底面未被卡片覆盖的部分用阴影表示.则图②中两块阴影部分的周长和是( ) 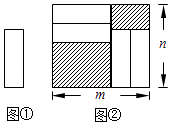
A.4n
B.4m
C.2(m+n)
D.4(m﹣n)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com