
分析 根据反比例函数的对称性,即关于原点对称和关于直线y=x对称,求出P点的坐标即可.
解答 解:∵反比例函数y=$\frac{6}{x}$的图象关于原点中心对称,
∴当点P与点D关于原点对称,则OD=OP,此时P点坐标为(-2,-3),
∵反比例函数y=的图象关于直线y=x对称,
∴点P与点D(2,3)关于直线y=x对称时满足OP=OD,此时P点坐标为(3,2),
点(3,2)关于原点的对称点也满足OP=OD,此时P点坐标为(-3,-2),
综上所述,P点的坐标为(-2,-3)或(3,2)或(-3,-2).
故答案为(-2,-3)或(3,2)或(-3,-2).
点评 本题考查的是反比例函数图象上点的坐标特征,反比例函数的对称性是本题的重点.


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
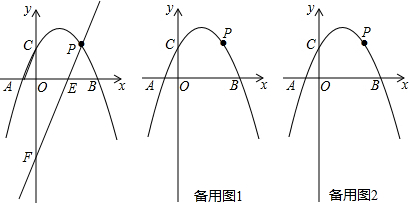
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
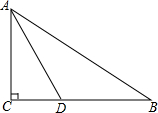 如图,在Rt△ABC中,∠C=90°,∠BAC的角平分线AD交BC边于点D.
如图,在Rt△ABC中,∠C=90°,∠BAC的角平分线AD交BC边于点D.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,AB半圆的直径,点O为圆心,OA=5,弦AC=8,OD⊥AC,垂足为E,交⊙O于D,连接BE.设∠BEC=α,则tanα的值为$\frac{3}{2}$.
如图,AB半圆的直径,点O为圆心,OA=5,弦AC=8,OD⊥AC,垂足为E,交⊙O于D,连接BE.设∠BEC=α,则tanα的值为$\frac{3}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com