
分析 先由y1的图象经过点A(1,1)可以求出m的值,然后根据y1+y2与y1为“同簇二次函数”就可以求出函数y2的表达式.
解答 解:∵y1的图象经过点A(1,1),y1=2x2-4mx+2m2+1,
∴2×12-4×m×1+2m2+1=1,
整理得:m2-2m+1=0,
解得:m1=m2=1,
∴y1=2x2-4x+3=2(x-1)2+1,
∴y1+y2=2x2-4x+3+ax2+bx+5=(a+2)x2+(b-4)x+8.
∵y1+y2与y1为“同簇二次函数”,
∴y1+y2=(a+2)(x-1)2+1=(a+2)x2-2(a+2)x+(a+2)+1,
其中a+2>0,即a>-2.
∴$\left\{\begin{array}{l}{b-4=-2(a+2)}\\{8=(a+2)+1}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=5}\\{b=-10}\end{array}\right.$,
∴函数y2的表达式为:y2=5x2-10x+5.
故答案为y2=5x2-10x+5.
点评 本题考查了求二次函数表达式以及二次函数一般式与顶点式之间相互转化,考查了二次函数的性质(开口方向、顶点坐标),考查了阅读理解能力.而对新定义的正确理解是解题的关键.


科目:初中数学 来源: 题型:解答题
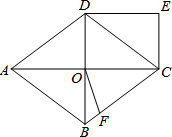 如图,菱形ABCD中,对角线AC,BD交于O点,DE∥AC,CE∥BD.
如图,菱形ABCD中,对角线AC,BD交于O点,DE∥AC,CE∥BD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
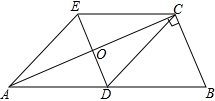 如图,△ABC中,∠BCA=90°,CD是边AB上的中线,分别过点C,D作BA,BC的平行线交于点E,且DE交AC于点O,连接AE.
如图,△ABC中,∠BCA=90°,CD是边AB上的中线,分别过点C,D作BA,BC的平行线交于点E,且DE交AC于点O,连接AE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
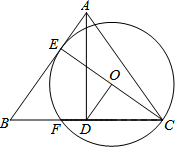 如图,在△ABC中,AB=AC,AD⊥BC于点D,过点C作⊙O与边AB相切于点E,交BC于点F,CE为⊙O的直径.
如图,在△ABC中,AB=AC,AD⊥BC于点D,过点C作⊙O与边AB相切于点E,交BC于点F,CE为⊙O的直径.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:关于x的一元二次方程-x2+(m+1)x+(m+2)=0(m>0).
已知:关于x的一元二次方程-x2+(m+1)x+(m+2)=0(m>0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
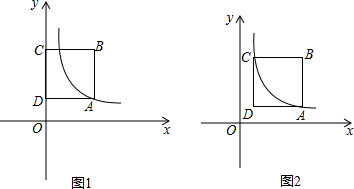
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
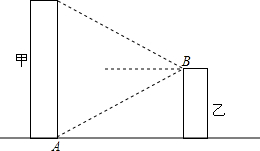 某城市搞亮化工程,如图,在甲楼底部,乙楼顶部分别安装一盏射灯.已知A灯恰好照到B灯,B灯恰好照到甲楼的顶部,如果两盏灯的光线与水平线的夹角相等,那么能否说甲楼的高度是乙楼的2倍?说说你的看法.
某城市搞亮化工程,如图,在甲楼底部,乙楼顶部分别安装一盏射灯.已知A灯恰好照到B灯,B灯恰好照到甲楼的顶部,如果两盏灯的光线与水平线的夹角相等,那么能否说甲楼的高度是乙楼的2倍?说说你的看法.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com