
【题目】已知抛物线![]() 与
与![]() 轴只有一个交点,以下四个结论:①抛物线的对称轴在
轴只有一个交点,以下四个结论:①抛物线的对称轴在![]() 轴左侧;②关于
轴左侧;②关于![]() 的方程
的方程![]() 有实数根;③
有实数根;③![]() ;④
;④![]() 的最大值为1.其中结论正确的为( )
的最大值为1.其中结论正确的为( )
A.①②③B.③④C.①③D.①③④
【答案】D
【解析】
根据 ![]() ,可知
,可知 ![]() <0可以判断①,再由抛物线与
<0可以判断①,再由抛物线与![]() 轴只有一个交点,可得抛物线大致的图象,根据二次函数的判别式为0,来计算出新方程的判别式即可得到方程根的情况,从而判断②.由x=1,x=-1应的函数值可以判断③和④.
轴只有一个交点,可得抛物线大致的图象,根据二次函数的判别式为0,来计算出新方程的判别式即可得到方程根的情况,从而判断②.由x=1,x=-1应的函数值可以判断③和④.
①抛物线的对称轴在y轴左侧,∵抛物线的对称轴为![]() ,∵
,∵ ![]() ,∴
,∴ ![]() <0,∴①正确.②关于
<0,∴①正确.②关于![]() 的方程
的方程![]() 有实数根抛物线,∵
有实数根抛物线,∵![]() 与
与![]() 轴只有一个交点,∴△=b-4ac=0,∴
轴只有一个交点,∴△=b-4ac=0,∴
△=b-4a(c+2)=-8a<0,∴方程![]() 无实根,∴②错误。③
无实根,∴②错误。③ ![]() ,由①可知抛物线顶点在x负半轴,∴当x=1时,可知抛物线x轴上方,∴
,由①可知抛物线顶点在x负半轴,∴当x=1时,可知抛物线x轴上方,∴![]() ,∴③正确。④由①x=-1时,y≥0,则有
,∴③正确。④由①x=-1时,y≥0,则有![]() ,∴
,∴![]() ,又∵c>0,∴
,又∵c>0,∴![]() 即
即![]() 的最大值为1,∴④正确,故选D.
的最大值为1,∴④正确,故选D.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】在一个箱子中有三个分别标有数字1,2,3的材质、大小都相同的小球,从中任意摸出一个小球,记下小球的数字x后,放回箱中并摇匀,再摸出一个小球,又记下小球的数字y。以先后记下的两个数字(x,y)作为点P的坐标。
(1)求点P的横坐标与纵坐标的和为4的概率,并画出树状图或列表;
(2)求点P落在以坐标原点为圆心、![]() 为半径的圆的内部的概率。
为半径的圆的内部的概率。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一位篮球运动员在距离篮圈中心水平距离![]() 处跳起投篮,球沿一条抛物线运动,当球运动的水平距离为
处跳起投篮,球沿一条抛物线运动,当球运动的水平距离为![]() 时,达到最大高度
时,达到最大高度![]() ,然后准确落入篮筐内,已知篮圈中心距离地面高度为
,然后准确落入篮筐内,已知篮圈中心距离地面高度为![]() ,试解答下列问题:
,试解答下列问题:
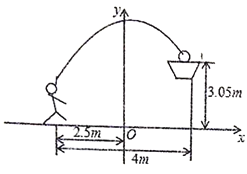
(1)建立图中所示的平面直角坐标系,求抛物线所对应的函数表达式.
(2)这次跳投时,球出手处离地面多高?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
在学习《圆》这一章时,老师给同学们布置了一道尺规作图题:
尺规作图:过圆外一点作圆的切线.
已知:P为⊙O外一点.
求作:经过点P的⊙O的切线.
小敏的作法如下:
如图,
(1)连接OP,作线段OP的垂直平分线MN交OP于点C;
(2)以点C为圆心,CO的长为半径作圆,交⊙O于A,B两点;
(3)作直线PA,PB.所以直线PA,PB就是所求作的切线.
老师认为小敏的作法正确.
请回答:连接OA,OB后,可证∠OAP=∠OBP=90°,其依据是_____;由此可证明直线PA,PB都是⊙O的切线,其依据是_____.
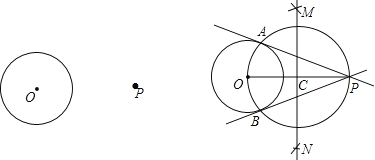
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠ACB为锐角.点D为射线BC上一动点,连接AD,将线段AD绕点A逆时针旋转90°得到AE,连结EC.如果AB=AC,∠BAC=90°.
①当点D在线段BC上时(与点B不重合),如图1,请你判断线段CE、BD之间的位置和数量关系(直接写出结论);
②当点D在线段BC的延长线上时,请你在图2画出图形,判断①中的结论是否仍然成立,并证明你的判断.

查看答案和解析>>
科目:初中数学 来源: 题型:
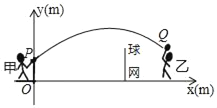
【题目】甲、乙两人进行羽毛球比赛,把球看成点,其飞行的路线为抛物线的一部分.如图建立平面直角坐标系,甲在O点正上方1m的P处发球,羽毛球飞行的高度y(m)与羽毛球距离甲站立位置(点O)的水平距离x(m)之间满足函败表达式y=a(x﹣4)2+h.已知点O与球网的水平距离为5m,球网的高度为1.55m,球场边界距点O的水平距离为10m.
(1)当a=﹣![]() 时,求h的值,并通过计算判断此球能否过网.
时,求h的值,并通过计算判断此球能否过网.
(2)若甲发球过网后,乙在另一侧距球网水平距离lm处起跳扣球没有成功,球在距球网水平距离lm,离地面高度2.2m处飞过,通过计算判断此球会不会出界?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,点C在⊙O上,延长BC至点D,使DC=CB,延长DA与⊙O的另一个交点为E,连接AC,CE.

(1)求证:∠B=∠D;
(2)若AB=4,BC﹣AC=2,求CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
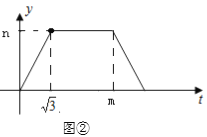
【题目】如图,在平行四边形ABCD中,∠D=60°,点M在线段AD上,DM= ![]() ,AM=2,点E从点D出发,沿着D-C-B-A匀速运动,速度为每秒2个单位长度,达到A点后停止运动,设△MDE的面积为y,点E运动的时间为t(s),y与t的部分函数关系如图②所示.
,AM=2,点E从点D出发,沿着D-C-B-A匀速运动,速度为每秒2个单位长度,达到A点后停止运动,设△MDE的面积为y,点E运动的时间为t(s),y与t的部分函数关系如图②所示.
(1)如图①中,DC=_____,如图②中,m=_______,n=_____.
(2)在E点运动过程中,将平行四边形沿ME所在直线折叠,则t为何值时,折叠后顶点D的对应点D′落在平行四边形的一边上.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的袋子中有1个红球,1个绿球和n个白球,这些球除颜色外无其他差别.
(1)从袋中随机摸出一个球,记录其颜色,然后放回.大量重复该实验,发现摸到绿球的频率稳定于0.25,求n的值;
(2)在该不透明袋子中同时摸出两个球,求摸出的两个球颜色不同的概率.(要求列表或画树状图)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com