
【题目】在![]() 中,
中,![]() ,点
,点![]() 为
为![]() 边的中点
边的中点
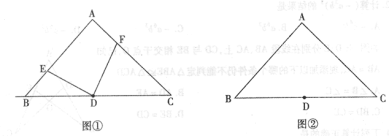
(1)如图①,点![]() 分别为边
分别为边![]() 上的点
上的点![]() ,且
,且![]() .若,则
.若,则![]()
![]() ;若
;若![]() ,则四边形
,则四边形![]() 的面积为
的面积为
(2)若点![]() 分别为
分别为![]() 延长线上的点,且
延长线上的点,且![]() ,那么
,那么![]() 吗?请利用图②说明理由.
吗?请利用图②说明理由.
【答案】(1)7, 25cm2;(2)![]() ,见解析
,见解析
【解析】
(1)连接AD,易知△ABC是等腰直角三角形,根据等腰直角三角形的性质可得AD=BD,∠FAD=∠B=45°,根据等角替换可得∠ADF=∠BDE,可得△BDE≌△ADF,根据全等三角形的性质可得BE=AF,进而可求CF,把四边形AEDF分割成△ADE和△ADF,即可求解.
(2)连接AD,根据等腰直角三角形的性质可得BD=AD,∠ABC=∠DAC=45°,再根据平角性质可得∠EBD=∠FAD=135°,根据等角替换可得∠ADF=∠BDE,根据全等三角形的判定证得△BDE≌△ADF,进而求证BE=AF.
(1)如图①,连接AD
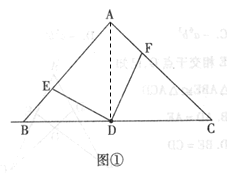
∵∠BAC=90°,AB=AC,
∴△ABC是等腰直角三角形,
∴∠B=45°,
∵D是BC的中点,
∴AD⊥BD,∠BAD=∠FAD=45°,
∴∠FAD=∠B=45°,
∵∠BDE+∠EDA=∠EDA+∠ADF=90°,
∴∠BDE=∠ADF,
∵∠BAD=∠B=45°,
∴AD=BD,
在△BDE和△ADF中
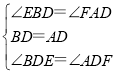
∴△BDE≌△ADF(ASA)
∴BE=AF
∵AB=AC=10cm,BE=3cm,
∴AF=BE=3cm
∴CF=10-3=7cm,
∵S△ABD=S△ACD=![]() S△ABC,
S△ABC,
即S△BDE+S△ADE=S△ADF+S△CDF
又∵△BDE≌△ADF
∴S△BDE=S△ADF
∴S△ADE=S△CDF,
∴S△ADE+S△ADF=![]() S△ABC=
S△ABC=![]() ×10×10=25cm2,
×10×10=25cm2,
即四边形AEDF的面积为25cm2
(2)结论:BE=AF
理由:如图②连接AD,
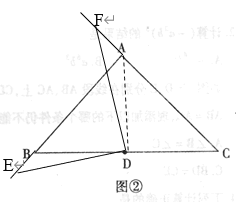
易知∠BDA=∠EDF=90°,
∴∠BDE+∠BDF=∠BDF+∠ADF,
∴∠BDE=∠ADF,
又∵D是BC的中点,△ABC是等腰直角三角形,
∴BD=AD,∠ABC=∠DAC=45°,
∴∠EBD=∠FAD=180°-45°=135°,
∴△BDE≌△ADF(ASA),
∴BE=AF


科目:初中数学 来源: 题型:
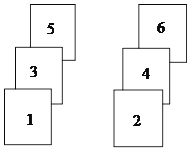
【题目】小明与小亮玩游戏,如图,两组相同的卡片,每组三张,第一组卡片正面分别标有数字1,3,5;第二组卡片正面分别标有数字2,4,6.他们将卡片背面朝上,分组充分洗匀后,从每组卡片中各摸出一张,称为一次游戏.当摸出的两张卡片的正面数字之积小于10,则小明获胜;当摸出的两张卡片的正面数字之积超过10,则小亮获胜.你认为这个游戏规则对双方公平吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)已知⊙O的直径为10cm,点A为⊙O外一定点,OA=12cm,点P为⊙O上一动点,求PA的最大值和最小值.
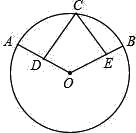
(2)如图:![]() =
=![]() ,D、E分别是半径OA和OB的中点.求证:CD=CE.
,D、E分别是半径OA和OB的中点.求证:CD=CE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列每一组数据中的三个数值分别为三角形的三边长:①3,4,5;②6,8,10;③5,12,13;④![]() ,2,
,2,![]() .其中不能构成直角三角形的是____(填序号).
.其中不能构成直角三角形的是____(填序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,完成任务:
自相似图形
定义:若某个图形可分割为若干个都与它相似的图形,则称这个图形是自相似图形.例如:正方形ABCD中,点E、F、G、H分别是AB、BC、CD、DA边的中点,连接EG,HF交于点O,易知分割成的四个四边形AEOH、EBFO、OFCG、HOGD均为正方形,且与原正方形相似,故正方形是自相似图形.
任务:
(1)图1中正方形ABCD分割成的四个小正方形中,每个正方形与原正方形的相似比为 ;
(2)如图2,已知△ABC中,∠ACB=90°,AC=4,BC=3,小明发现△ABC也是“自相似图形”,他的思路是:过点C作CD⊥AB于点D,则CD将△ABC分割成2个与它自己相似的小直角三角形.已知△ACD∽△ABC,则△ACD与△ABC的相似比为 ;
(3)现有一个矩形ABCD是自相似图形,其中长AD=a,宽AB=b(a>b).
请从下列A、B两题中任选一条作答:我选择 题.
A:①如图3﹣1,若将矩形ABCD纵向分割成两个全等矩形,且与原矩形都相似,则a= (用含b的式子表示);
②如图3﹣2若将矩形ABCD纵向分割成n个全等矩形,且与原矩形都相似,则a= (用含n,b的式子表示);
B:①如图4﹣1,若将矩形ABCD先纵向分割出2个全等矩形,再将剩余的部分横向分割成3个全等矩形,且分割得到的矩形与原矩形都相似,则a= (用含b的式子表示);
②如图4﹣2,若将矩形ABCD先纵向分割出m个全等矩形,再将剩余的部分横向分割成n个全等矩形,且分割得到的矩形与原矩形都相似,则a= (用含m,n,b的式子表示).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com