

分析 (1)利用抛物线解析式求出点A、C坐标,求出线段OA、AC长度,即可求出∠ACO的正弦值;
(2)首先设出点D坐标,写出点H坐标,利用相似三角形比例关系可求出线段DE的长,根据CH:BH=2:1,求出线段DE的长;
(3)设出点P坐标,写出直线PM解析式,表示出点M、及与y轴交点坐标,利用三角形面积求出点P坐标.
解答 解(1)令x=0,y=4,
∴C(0,4),OC=4,
令y=0,x1=-1,x2=3,
∴A(-1,0),B(3,0),OA=1,
∴AC=$\sqrt{16+1}$=$\sqrt{17}$,
sin∠ACO=$\frac{OA}{AC}$=$\frac{1}{\sqrt{17}}$=$\frac{\sqrt{17}}{17}$.
2)如图1,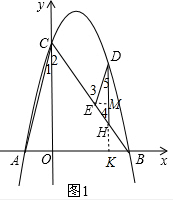
∵DE∥AC,
∴∠1+∠2=∠3=∠4+∠5,
∵DH∥y轴,
∴∠2=∠4,
∴∠1=∠5,
∴OA:OC=EM:DM,
过点E作EM⊥DH,垂足为M,
设点D(m,-$\frac{4}{3}$m2+$\frac{8}{3}$m+4),
直线BC:y=-$\frac{4}{3}$x+4,
∴H(m,-$\frac{4}{3}$m+4),
∴DH=-$\frac{4}{3}$m2+4m,
设EM=x,则DM=4x,
∠MEH=∠B,
∴HM=$\frac{4}{3}$x,DH=$\frac{4}{3}$x+4x=$\frac{16}{3}$x,
∴x=$\frac{3DH}{16}$,
∴DE=$\sqrt{17}$x=$\frac{3\sqrt{17}DH}{16}$=$\frac{3\sqrt{17}}{16}$(-$\frac{4}{3}$m2+4m)=-$\frac{\sqrt{17}}{4}$m2+$\frac{3\sqrt{17}}{4}$m,
当CH:BH=2:1时,
延长DH至点K,则OK:KB=2:1,
OK=2,
∴m=2.
∴DE=-$\sqrt{17}$+$\frac{3\sqrt{17}}{2}$=$\frac{\sqrt{17}}{2}$.
(3)P(1,0)、(2$\sqrt{2}$+1,0)、(1-2$\sqrt{2}$,0).
直线BC解析式为:y=-$\frac{4}{3}$x+4,
直线AC解析式为:y=4x+4,
∵作PM∥BC交直线AC于点M,
∴设PM直线解析式为y=-$\frac{4}{3}$x+b,
∴P($\frac{3b}{4}$,0)
联立直线AC,求得M($\frac{3b-12}{16}$,$\frac{3b+4}{4}$),
当点P在线段AB上时,如图: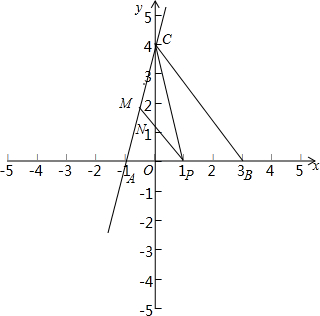
∴S△CPM=$\frac{1}{2}$×CN×($\frac{3b}{4}$-$\frac{3b-12}{4}$)=2
∴$\frac{1}{2}$×(4-b)×($\frac{3b}{4}$-$\frac{3b-12}{16}$)=2
解得:b=$\frac{4}{3}$,
∴P(1,0);
当点P在线段AB上,
连接CP,是否存在点P使S△CPM=2
当点P在线段AB延长线上时,如图: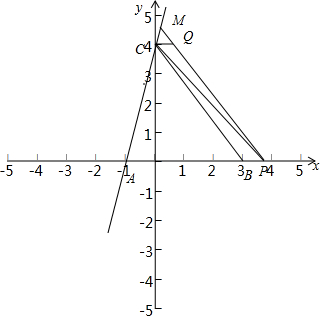
同理:P($\frac{3b}{4}$,0),M($\frac{3b-12}{16}$,$\frac{3b+4}{4}$),
做CQ⊥y轴,Q($\frac{3b-12}{4}$,4)
∴S△CPM=$\frac{1}{2}$×CQ×$\frac{3b-12}{4}$=2
解得:b=$\frac{8\sqrt{2}+4}{3}$,
∴P(2$\sqrt{2}$+1,0).
当点P在线段BA延长线上时,如图: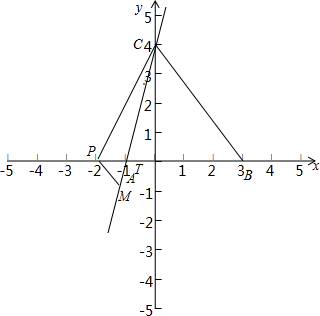
同理:P($\frac{3b}{4}$,0),M($\frac{3b-12}{16}$,$\frac{3b+4}{4}$),
∴S△CPM=$\frac{1}{2}$×PA×(4-$\frac{3b+4}{4}$)=2
解得:b=$\frac{4-8\sqrt{2}}{3}$,
∴P(1-2$\sqrt{2}$,0).
综上所述:P(1,0)、(2$\sqrt{2}$+1,0)、(1-2$\sqrt{2}$,0).
点评 题目考查了二次函数综合应用,考查知识点包括一次函数二次函数解析式求解、相似三角形、三角形面积求解等知识点,题目整体较难,适合学生进行中考二次函数压轴训练.


科目:初中数学 来源: 题型:解答题
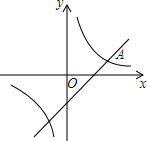 如图,在平面直角坐标系xOy中,双曲线y=$\frac{m}{x}$与直线y=kx-2交于点A(3,1).
如图,在平面直角坐标系xOy中,双曲线y=$\frac{m}{x}$与直线y=kx-2交于点A(3,1).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图1,在△ABC中,AB=AC,点D是BC的中点,点E在AD上.
如图1,在△ABC中,AB=AC,点D是BC的中点,点E在AD上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
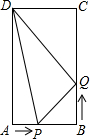 如图,在矩形ABCD中,AB=6cm,BC=12cm,点P从点A沿边AB向终点B以1cm/s的速度移动;同时,点Q从点B沿边BC向终点C以2cm/s的速度移动.设移动时间为t秒,解答下列问题:
如图,在矩形ABCD中,AB=6cm,BC=12cm,点P从点A沿边AB向终点B以1cm/s的速度移动;同时,点Q从点B沿边BC向终点C以2cm/s的速度移动.设移动时间为t秒,解答下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com