
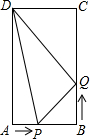
 如图,在矩形ABCD中,AB=6cm,BC=12cm,点P从点A沿边AB向终点B以1cm/s的速度移动;同时,点Q从点B沿边BC向终点C以2cm/s的速度移动.设移动时间为t秒,解答下列问题:
如图,在矩形ABCD中,AB=6cm,BC=12cm,点P从点A沿边AB向终点B以1cm/s的速度移动;同时,点Q从点B沿边BC向终点C以2cm/s的速度移动.设移动时间为t秒,解答下列问题:分析 (1)根据代数式的定义列出代数式即可.
(2)根据运动速度表示出长度和三角形面积公式列出方程.
(3)根据运动速度表示出长度和三角形面积公式列出方程;
(4)根据等腰三角形的判定求出不同情况下的解.
解答 解:(1)设移动时间为t秒,AP=t,BP=6-t,BQ=2t,CQ=12-2t;
故答案为:t;6-t;2t;12-2t;
(2)由题意得:$\frac{1}{2}$×(6-t)×2t=8
∴t=2或t=4
∴当t=2或t=4时△PBQ的面积等于8cm2;
(3)由题意得:$6×12-\frac{1}{2}×12×t-\frac{1}{2}×6×(12-2t)-$$\frac{1}{2}$×(6-t)×2t=31
可得:t2-6t+5=0,
∴t=1或t=5
∴当t=1或t=5时△DPQ的面积为31cm2,
(4)①当DP=DQ时,由题意得122+t2=62+(12-2t)2,
解得:${t}_{1}=8-2\sqrt{13},{t}_{2}=8+2\sqrt{13}$(舍去)
②当DP=PQ时,由题意得122+t2=(6-t)2+(2t)2,
解得${t}_{1}=\frac{3-3\sqrt{13}}{2}(舍去),{t}_{2}=\frac{3+3\sqrt{13}}{2}$(舍去),
③当DQ=PQ时,由题意得62+(12-2t)2=(6-t)2+(2t)2,
解得${t}_{1}=6\sqrt{13}-18,{t}_{2}=-6\sqrt{13}-18$(舍去),
综上所述,当t为$8-2\sqrt{13}$,或$6\sqrt{13}-18$时,△PDQ等腰三角形
点评 本题考查矩形的性质,三角形的面积以及等腰三角形的判定定理,能够熟练掌握矩形的性质并能进行一些简单的计算.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
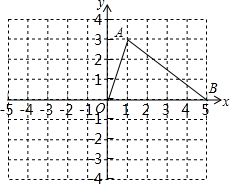 如图,网格中每个小正方形的顶点叫格点,△OAB的顶点的坐标分别为O(0,0)、A(1,3)、B(5,0).
如图,网格中每个小正方形的顶点叫格点,△OAB的顶点的坐标分别为O(0,0)、A(1,3)、B(5,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
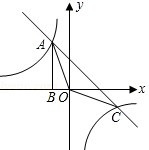 如图,Rt△ABO的顶点A是双曲线y1=$\frac{k}{x}$与直线y2=-x-(k+1)在第二象限的交点.AB⊥x轴于B,且S△ABO=$\frac{3}{2}$.
如图,Rt△ABO的顶点A是双曲线y1=$\frac{k}{x}$与直线y2=-x-(k+1)在第二象限的交点.AB⊥x轴于B,且S△ABO=$\frac{3}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 点O到△ABC的三顶点的距离一定相等 | |
| B. | ∠C的平分线一定经过点O | |
| C. | 点O到△ABC的三边距离一定相等 | |
| D. | 点O一定在△ABC的内部 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知四边形ABCD的对角线AC、BD交于点F,点E是BD上一点,且∠BCA=∠ADE,∠CAD=∠BAE.
如图,已知四边形ABCD的对角线AC、BD交于点F,点E是BD上一点,且∠BCA=∠ADE,∠CAD=∠BAE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com