练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    1．如图，古希腊人常用小石子在沙滩上摆成各种形状来研究数．例如：称图中的数1，5，12，22…为五边形数，则第7个五边形数是（　　）
    A．62B．70C．84D．108

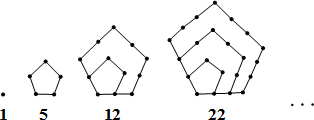
    分析 观察图形得到第1个五边形数为1，第2个五边形数为1+4=5，第3个五边形数为1+4+7=12，第4个五边形数为1+4+7+10=22，即每个五边形数是从1开始，后面的数都比前面一个数大3的几个数的和，且数的个数等于序号数，则第7个五边形数为1+4+7+10+13+16+19=70．

    解答 解：∵第1个五边形数为1，
    第2个五边形数为1+4=5，
    第3个五边形数为1+4+7=12，
    第4个五边形数为1+4+7+10=22，
    ∴第5个五边形数为1+4+7+10+13=35，
    第6个五边形数为1+4+7+10+13+16=51，
    第7个五边形数为1+4+7+10+13+16+19=70．
    故选：B．

    点评 本题考查了图形的变化规律，通过从一些特殊的图形变化中发现不变的因素或按规律变化的因素，然后推广到一般情况．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

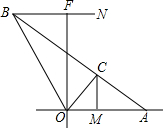    5．如图，一轮渡从B点出发沿东偏南25°方向匀速航行，经过4.5分钟后达到C处，若保持航线不变，继续航行可直接到达停靠码头A，在停靠码头A的正西反向500m处有一观察站O，在O处测得B位于其北偏西35°，C位于其北偏东55°．求C处到海岸线OA的距离大约是多少米？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．已知实数a、b、c在数轴上的位置如图所示，试化简：$\sqrt{{{（-c）}^2}}-|{a-c}|+\sqrt{{{（a+b）}^2}}-|{b+c}|$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．如图，有一张边长为6$\sqrt{2}$cm的正方形纸板，现将该纸板的四个角剪掉，制作一个有底无盖的长方体盒子，剪掉的四个角是面积相等的小正方形，此小正方形的边长为$\sqrt{2}$cm．求：
    （1）剪掉四个角后，制作长方体盒子的纸板的面积；
    （2）长方体盒子的体积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．现用棱长为2cm的小立方体按如图所示规律搭建几何体，图中自上面下分别叫第一层、第二层、第三层…，其中第一层摆放1个小立方体，第二层摆放3个小立方体，第三层摆放6个小立方体…，那么搭建第1个小立方体，搭建第2个几何体需要4个小立方体，搭建第3个几何体需要10个小立方体…，按此规律继续摆放．
    （1）搭建第4个几何体需要小立方体的个数为20；
    （2）为了美观，需将几何体的所有露出部分（不包含底面）都喷涂油漆，且喷涂1cm2需用油漆0.3克．
    ①求喷涂第4个几何体需要油漆多少克？
    ②如果要求从第1个几何体开始，依此对第1个几何体，第2个几何体，第3和几何体，…，第n个几何体（其中n为正整数）进行喷涂油漆，那么当喷涂完第20个几何体时，共用掉油漆多少克？
    【参考公式：①1×2+2×3+3×4+…+n（n+1）=$\frac{n（n+1）（n+2）}{3}$；
    ②12+22+32+…+n2=$\frac{n（n+1）（2n+1）}{6}$，其中n为正整数】

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    6．在△ABC中，H是高AD、BE所在直线的交点，且BH=AC，则∠ABC的度数为45°或135°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    13．如图，O为△ABC的外心，△OCP为正三角形，OP与AC相交于D点，连接OA．若∠BAC=69°14′，AB=AC，则∠ADP的度数85°23′．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    10．下列方程组中，是二元一次方程组的是（　　）
    A．$\left\{\begin{array}{l}xy=1\\ x-y=2\end{array}$B．$\left\{\begin{array}{l}5x-2y=3\\ \frac{1}{x}-y=3\end{array}$C．$\left\{\begin{array}{l}2x-z=0\\ 3x-y=\frac{1}{5}\end{array}$D．$\left\{\begin{array}{l}x=5\\ \frac{x}{2}-\frac{y}{3}=7\end{array}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

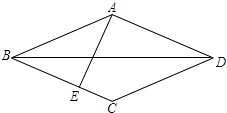    11．已知：如图，在菱形ABCD中，AE⊥BC，垂足为E，对角线BD=4，tan∠CBD=$\frac{1}{2}$，则AB=$\sqrt{5}$，sin∠ABE=$\frac{4}{5}$．

    查看答案和解析>>

    同步练习册答案