
【题目】如图,在Rt△ABC中,∠BAC=90°,过顶点A的直线DE∥BC,∠ABC,∠ACB的平分线分别交DE于点E、D,若AC=3, BC=5,则DE的长为____.

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,轮船从A港出发,以28海里/小时的速度向正北方向航行,此时测的灯塔M在北偏东30°的方向上.半小时后,轮船到达B处,此时测得灯塔M在北偏东60°的方向上.
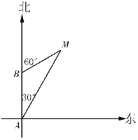
(1)求轮船在B处时与灯塔M的距离;
(2)轮船从B处继续沿正北方向航行,又经半小时后到达C处.求:此时轮船与灯塔M的距离是多少?灯塔M在轮船的什么方向上?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A的坐标为(1,0),以线段OA为边在第四象限内作等边三角形AOB,点C为x正半轴上一动点(OC>1),连接BC,以线段BC为边在第四象限内作等边△CBD,连接DA并延长,交y轴于点E.
①△OBC与△ABD全等吗?判断并证明你的结论;
②当点C运动到什么位置时,以A,E,C为顶点的三角形是等腰三角形?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=ax2+bx+4的图象与x轴交于点B(-2,0),点C(8,0),与y轴交于点A.
(1)求二次函数y=ax2+bx+4的表达式;
(2)连接AC,AB,若点N在线段BC上运动(不与点B,C重合),过点N作NM∥AC,交AB于点M,当△AMN面积最大时,求N点的坐标;
(3)连接OM,在(2)的结论下,求OM与AC的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC中,∠C=90°, BC=10,AC=6,过点A作BC的平行线l,P为直线l上的动点,且△BCP是等腰三角形,则AP的长为_____

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A,B是⊙O上的两点,∠AOB=120°,C是![]() 的中点.
的中点.
(1)如图1,求∠A的度数;
(2)如图2,延长OA至点D,使OA=AD,连接DC,延长OB交DC的延长线于点E.若⊙O的半径为1,求DE的长.

图1 图2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个大正方形和四个全等的小正方形按图①、②两种方式摆放,设小正方形的边长为x,请仔细观察图形回答下列问题.
(1)用含a、b的代数式表示x,则x= .
(2)用含a、b的代数式表示大正方形的边长 .(请将结果化为最简)
(3)利用前两问的结论求出图②的大正方形中未被小正方形覆盖部分的面积.(用a、b的代数式表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,CD切⊙O于点C,与BA的延长线交于点D,OE⊥AB交⊙O于点E,连接CA、CE、CB,CE交AB于点G,过点A作AF⊥CE于点F,延长AF交BC于点P.
(Ⅰ)求∠CPA的度数;
(Ⅱ)连接OF,若AC=![]() ,∠D=30°,求线段OF的长.
,∠D=30°,求线段OF的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com