
����Ŀ��������ڼ䣬�����н�����һ���±��������ۣ���֪����4�м�Ʒ���±���6����Ʒ���±���260Ԫ������5�м�Ʒ���±���4����Ʒ���±���220Ԫ.��������Ʒ���±�����ͬ���ۼ����ۣ���Ʒ���±�������![]() ���У����ۼ�
���У����ۼ�![]() ��Ԫ��֮��Ĺ�ϵΪ
��Ԫ��֮��Ĺ�ϵΪ![]() �����ۼ�Ϊ40Ԫʱ����Ʒ���±�������100�У��ۼ�ÿ���1Ԫ��������5��.
�����ۼ�Ϊ40Ԫʱ����Ʒ���±�������100�У��ۼ�ÿ���1Ԫ��������5��.
��1�����������Ʒ���±�ÿ�еĽ��۷ֱ�Ϊ����Ԫ��
��2������Ʒ���±����ۼ�Ϊ����Ԫʱ����Ʒ���±����������������ʱ��������Ʒ���±�������������Ϊ���٣�
��3������Ʒ���±���������������Ʒ���±�����������![]() ����ʹ����Ʒ���±�����������ߣ����ʱ�Ķ���Ϊ���٣�
����ʹ����Ʒ���±�����������ߣ����ʱ�Ķ���Ϊ���٣�
���𰸡���1����Ʒ�ƽ���Ϊ20Ԫ����Ʒ�ƽ���Ϊ30Ԫ����2������Ʒ������������Ϊ2125Ԫ����3����x=36ʱ��ȡ�����ֵ.
��������
��1�����������г����������Ʒ�ƺ���Ʒ�ƵĽ���.
��2���������W��![]() ��������л���Ϊ�������µĶ���ʽ��������ҵ��ۼ������������.
��������л���Ϊ�������µĶ���ʽ��������ҵ��ۼ������������.
��3�����ݲ���ʽ400-8x��300-5x��W��![]() ������⣬�õ���ʱ�Ķ���.
������⣬�õ���ʱ�Ķ���.
��1���⣺���Ʒ�ƽ���ΪaԪ����Ʒ�ƽ���ΪbԪ��
������ɵ�![]()
���![]()
��2���������![]()
![]()
![]()
���ۼ�Ϊ45Ԫʱ����Ʒ���±�������������ߣ�Ϊ1125Ԫ
���ۼ�Ϊ45Ԫʱ����Ʒ���±���������Ϊ![]() Ԫ
Ԫ
����Ʒ������������Ϊ2125Ԫ
��3���ɲ���ʽ400-8x��300-5x����x��36��
��![]()
![]()
������öԳ���Ϊ505/13��
����x=36ʱ��ȡ�����ֵ.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪![]() ��
��![]() ��ֱ������
��ֱ������![]() ����
����![]() ������
������![]() �ڵ�
�ڵ�![]() ����
����![]() �ڵ�
�ڵ�![]() ����ʹ
����ʹ![]() .
.
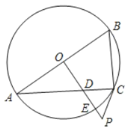
��1����֤��![]() ��
��![]() �����ߣ�
�����ߣ�
��2����![]() ��
��![]() ����
����![]() �ij�.
�ij�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����֪��E��F��G��H�Ǿ���ABCD���ߵ��е㣬AB��2.4��BC��3.4������M�ӵ�A��������A��B��C��D��A�����˶�������Aֹͣ�����M�˶���·��Ϊx����M���ı���EFGH��ijһ������ľ���Ϊy�������ʾy����x�ĺ�����ϵ��ͼ����ͼ2��ʾ����ô�ı���EFGH����������ǣ�������
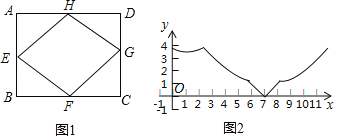
A. ��EB. ��FC. ��GD. ��H
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
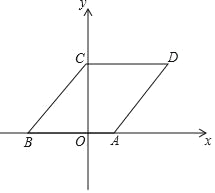
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�����ABCD�ı�AB��x���ϣ���B���꣨��3��0������C��y���������ϣ���sin��CBO=![]() ����P��ԭ��O��������ÿ��һ����λ���ȵ��ٶ���x���������ƶ����ƶ�ʱ��Ϊt��0��t��5���룬����P��ƽ����y���ֱ��l��ֱ��lɨ���ı���OCDA�����ΪS��
����P��ԭ��O��������ÿ��һ����λ���ȵ��ٶ���x���������ƶ����ƶ�ʱ��Ϊt��0��t��5���룬����P��ƽ����y���ֱ��l��ֱ��lɨ���ı���OCDA�����ΪS��
��1�����D���꣮
��2����S����t�ĺ�����ϵʽ��
��3����ֱ��l�ƶ������У�l���Ƿ����һ��Q��ʹ��B��C��QΪ������������ǵ���ֱ�������Σ������ڣ�ֱ��д��Q������ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
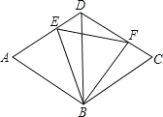
����Ŀ����ͼ,�߳�Ϊ2������ABCD��,BD=2,E��F�ֱ���AD,CD�ϵĶ���(�����˵�)����AE+CF=2�����߶�EF������Сֵ��__________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
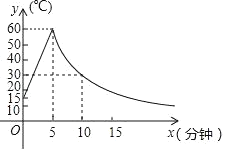
����Ŀ��������ij�����Ͳ��Ͻ��мӹ�������Ҫ������£�ʹ���ֲ��ϱ�����һ���¶ȷ�Χ�ڷ��ɼӹ�����ͼ�������ֲ��ϵļӹ������У��ò��ϵ��¶�y������ʱ��x��min���仯����ͼ����֪�ò��ϣ���ʼ�¶�Ϊ15�������¶������Σ�y��x��һ�κ�����ϵ���ڵ�5�����¶ȴﵽ60����ֹͣ���£����¶��½��Σ�y��x�ɷ�������ϵ��
��1��д���ò����¶��������½��Σ�y��x�ĺ�����ϵʽ��
�������Σ���0��x��5ʱ��y���� ����
���½��Σ���x��5ʱ��y�� ����
��2�����ݹ���Ҫ�����ϵ��¶Ȳ�����30�������Խ��в�Ʒ�ӹ���������ͼ����ʾ���¶ȱ仯�����У����Խ��мӹ��ʱ�䣿
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y=ax2+bx+c(a��0)��ͼ����ͼ��ʾ,���н��ۣ���2a+b<0;��abc>0;��4a2b+c>0;��a+c>0,������ȷ���۵ĸ���Ϊ( )

A. 1�� B. 2�� C. 3�� D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ǰ�a��b�������н�С��������min{a��b}��ֱ��y=kx��k��2��k��0���뺯��y=min{x2��1����x+1}��ͼ������ֻ��2�����㣬��k��ȡֵΪ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪�����ߵĶ���ΪA��0��1��������CDEF�Ķ���C��F���������ϣ���D��E��x���ϣ�CF��y���ڵ�B��0��2�����Ҿ��������Ϊ8���������ߵĽ���ʽ��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com