
科目: 来源: 题型:
【题目】某玩具厂有4个车间,某周是质量检查周,现每个车间都原有a(a>0)个成品,且每个车间每天都生产b(b>0)个成品,质量科派出若干名检验员周一、周二检验其中两个车间原有的和这两天生产的所有成品,然后,周三到周五检验另外两个车间原有的和本周生产的所有成品,假定每名检验员每天检验的成品数相同.
(1)这若干名检验员1天共检验多少个成品?(用含a、b的代数式表示)
(2)若一名检验员1天能检验![]() b个成品,则质量科至少要派出多少名检验员?
b个成品,则质量科至少要派出多少名检验员?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,将矩形纸片ABCD折叠,使点D与点B重合,点C落在C′处,折痕为EF,若AB=1,BC=2,则△ABE和△BC′F的周长之和为( )

A. 3 B. 4 C. 6 D. 8
查看答案和解析>>
科目: 来源: 题型:
【题目】种植草莓大户张华现有22吨草莓等待出售,有两种销售渠道,一是运往省城直接批发给零售商,二是在本地市场零售,受客观因素影响,张华每天只能采用一种销售渠道,而且草莓必须在10天内售出(含10天)经过调查分析,这两种销售渠道每天销量及每吨所获纯利润见右表:
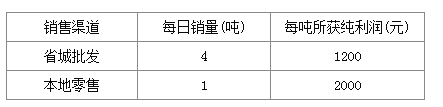
(1)若一部分草莓运往省城批发给零售商,其余在本地市场零售,请写出销售22吨草莓所获纯利润y(元)与运往省城直接批发零售商的草莓量x(吨)之间的函数关系式;
(2)怎样安排这22吨草莓的销售渠道,才使张华所获纯利润最大?并求出最大纯利润.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知y是关于x的一次函数,且当x=3时,y=-2;当x=2时,y=-3.
(1)求这个一次函数的表达式;
(2)求当x=-3时,函数y的值;
(3)求当y=2时,自变量x的值;
(4)当y>1时,自变量x的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】小明骑单车上学,当他骑了一段路时,想起要买某本书,于是又折回到刚经过的某书店,买到书后继续去学校以下是他本次上学所用的时间与路程的关系示意图.

根据图中提供的信息回答下列问题:
(1)小明家到学校的路程是________米
(2)小明在书店停留了___________分钟.
(3)本次上学途中,小明一共行驶了________ 米,一共用了______ 分钟.
(4)在整个上学的途中_________(哪个时间段)小明骑车速度最快,最快的速度是___________米/分.
查看答案和解析>>
科目: 来源: 题型:
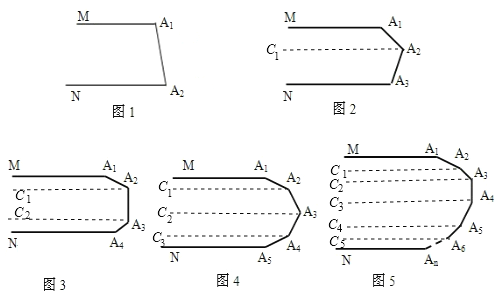
【题目】(1) 如图1,MA1∥NA2,则∠A1+∠A2=_________度.
如图2,MA1∥NA3,则∠A1+∠A2+∠A3=_________ 度.
如图3,MA1∥NA4,则∠A1+∠A2+∠A3+∠A4=_________度.
如图4,MA1∥NA5,则∠A1+∠A2+∠A3+∠A4+∠A5=_________度.
如图5,MA1∥NAn,则∠A1+∠A2+∠A3+…+∠An=_________ 度.

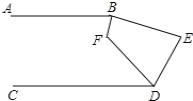
(2) 如图,已知AB∥CD,∠ABE和∠CDE的平分线相交于F,∠E=80°,求∠BFD的度数.

【答案】(1) 180; 360; 540;720;180(n-1);(2)140°.
【解析】试题分析:(1)首先过各点作MA 1 的平行线,由MA 1 ∥NA 2 ,可得各线平行,根据两直线平行,同旁内角互补,即可求得答案;
(2)由(1)中的规律可得∠ABE+∠E+∠CDE=360°,所以∠ABE+∠CDE=360°-80°=280°,又因为BF、DF平分∠ABE和∠CDE,所以∠FBE+∠FDE=140°,又因为四边形的内角和为360°,进而可得答案.
试题解析:(1)如图1,
∵MA 1 ∥NA 2 ,
∴∠A 1 +∠A 2 =180°.
如图2,过点A 2 作A 2 C 1 ∥A 1 M,
∵MA 1 ∥NA 3 ,
∴A 2 C 1 ∥A 1 M∥NA 3 ,
∴∠A 1 +∠A 1 A 2 C 1 =180°,∠C 1 A 2 A 3 +∠A 3 =180°,
∴∠A 1 +∠A 2 +∠A 3 =360°.
如图3,过点A 2 作A 2 C 1 ∥A 1 M,过点A 3 作A 3 C 2 ∥A 1 M,
∵MA 1 ∥NA 3 ,
∴A 2 C 1 ∥A 3 C 2 ∥A 1 M∥NA 3 ,
∴∠A 1 +∠A 1 A 2 C 1 =180°,∠C 1 A 2 A 3 +∠A 2 A 3 C 2 =180°,∠C 2 A 3 A 4 +∠A 4 =180°,
∴∠A 1 +∠A 2 +∠A 3 +∠A 4 =540°.
如图4,过点A 2 作A 2 C 1 ∥A 1 M,过点A 3 作A 3 C 2 ∥A 1 M,
∵MA 1 ∥NA 3 ,
∴A 2 C 1 ∥A 3 C 2 ∥A 1 M∥NA 3 ,
∴∠A 1 +∠A 1 A 2 C 1 =180°,∠C 1 A 2 A 3 +∠A 2 A 3 C 2 =180°,∠C 2 A 3 A 4 +∠A 3 A 4 C 3 =180°,∠C 3 A 4 A 5 +∠A 5 =180°,
∴∠A 1 +∠A 2 +∠A 3 +∠A 4 +∠A 5 =720°;
从上述结论中你发现了规律:如图5,MA 1 ∥NA n ,则∠A 1 +∠A 2 +∠A 3 +…+∠A n =180(n-1)度,
故答案为:180,360,540,720,180(n-1);
(2)由(1)可得∠ABE+∠E+∠CDE=360°,
∵∠E=80°,
∴∠ABE+∠CDE=360°-80°=280°,
又∵BF、DF平分∠ABE和∠CDE,
∴∠FBE+∠FDE=140°,
∵∠FBE+∠E+∠FDE+∠BFD=360°,
∴∠BFD=360°-80°-140°=140°.
【点睛】本题考查了平行线的性质:两直线平行,同旁内角互补、四边形的内角和是360°,解题的关键是,(1)小题正确添加辅助线,发现规律:MA 1 ∥NA n ,则∠A 1 +∠A 2 +∠A 3 +…+∠A n =180(n-1)度;(2)小题能应用(1)中发现的规律.
【题型】解答题
【结束】
28
【题目】已知如图1,线段AB、CD相交于点O,连结AC、BD,我们把形如图1的图形称之为“8字形”,那么在这一个简单的图形中,到底隐藏了哪些数学知识呢?下面就请你发挥聪明才智,解决以下问题:

(1)在图1中,请写出∠A、∠B、∠C、∠D之间的数量关系,并说明理由;
(2)仔细观察,在图2中“8字形”的个数有 个;
(3)在图2中,若∠B=76°,∠C=80°,∠CAB和∠BDC的平分线AP和DP相交于点P,并且与CD、AB分别相交于M、N利用(1)的结论,试求∠P的度数;
(4)在图3中,如果∠B和∠C为任意角,并且AP和DP分别是∠CAB和∠BDC的三等分线,即∠PAO=![]() ∠CAO, ∠BDP=
∠CAO, ∠BDP=![]() ∠BOD,那么∠P与∠C、∠B之间存在的数量关系是 (直接写出结论即可).
∠BOD,那么∠P与∠C、∠B之间存在的数量关系是 (直接写出结论即可).
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知△ABC内接于⊙O,且AB=AC,直径AD交BC于点E,F是OE上的一点,使CF∥BD.
(1)求证:BE=CE;
(2)试判断四边形BFCD的形状,并说明理由;
(3)若BC=8,AD=10,求CD的长.

查看答案和解析>>
科目: 来源: 题型:
【题目】(1)填空21-20=2( ); 22-21=2( ) ;23 -22=2( )
(2)请用字母表示第n个等式,并验证你的发现.
(3)利用(2)中你的发现,求20+21+22+23+…+22016+22017的值.
【答案】(1)0,1,2;(2)证明见解析;(3)![]()
【解析】试题分析:(1)根据0次幂的意义和乘方的意义进行计算即可;
(2)观察各等式得到2的相邻两个非负整数幂的差等于其中较小的2的非负整数幂,即2n-2n-1=2n-1(n为正整数);
(3)由于21-20=20,22-21=21,23-22=22,…22018-22017=22017,然后把等式左边与左边相加,右边与右边相加即可求解.
试题解析:(1)21-20=1=20;22-21=2=21;23-22=4=22,
故答案为:0,1,2;
(2)观察可得:2n-2n-1=2n-1(n为正整数),证明如下:
2n-2n-1=2×2n-1-2n-1=2n-1×(2-1)=2n-1;
(3)∵21-20=20,
22-21=21,
23-22=22,
…
22018-22017=22017,
∴22018-20=20+21+22+23+…+22016+22017,
∴20+21+22+23+…+22016+22017的值为22018-1.
【题型】解答题
【结束】
27
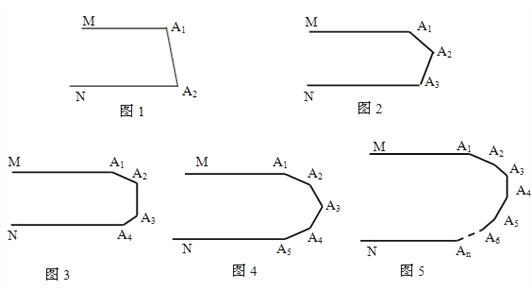
【题目】(1) 如图1,MA1∥NA2,则∠A1+∠A2=_________度.
如图2,MA1∥NA3,则∠A1+∠A2+∠A3=_________ 度.
如图3,MA1∥NA4,则∠A1+∠A2+∠A3+∠A4=_________度.
如图4,MA1∥NA5,则∠A1+∠A2+∠A3+∠A4+∠A5=_________度.
如图5,MA1∥NAn,则∠A1+∠A2+∠A3+…+∠An=_________ 度.
(2) 如图,已知AB∥CD,∠ABE和∠CDE的平分线相交于F,∠E=80°,求∠BFD的度数.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知,如图, AB∥CD,∠1=∠2,那么∠E和∠F相等吗? 为什么?
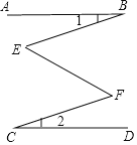
【答案】相等,理由见解析.
【解析】试题分析:分别过E、F 点作CD的平行线EM、FN,根据平行线的性质得CD∥FN∥EM∥AB,则∠3=∠1,∠4=∠5,∠1=∠6,而∠1=∠2,于是3+∠4=∠5+∠6.
试题解析:分别过E、F 点作CD的平行线EM、FN,如图
∵AB∥CD,
∴CD∥FN∥EM∥AB,
∴∠3=∠2,∠4=∠5,∠1=∠6,
而∠1=∠2,
∴∠3+∠4=∠5+∠6,
即∠BEF=∠EFC.

【题型】解答题
【结束】
26
【题目】(1)填空21-20=2( ); 22-21=2( ) ;23 -22=2( )
(2)请用字母表示第n个等式,并验证你的发现.
(3)利用(2)中你的发现,求20+21+22+23+…+22016+22017的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com